

 |
 |
Соотношения, связывающие термодинамические параметры среды до и после ударной волны, приобретают наиболее простой и законченный вид для так называемого совершенного газа, т.е. газа с постоянным значением γ – отношения теплоемкости при постоянном давлении к теплоемкости при постоянном объеме. В этом случае возбуждаются только поступательные и вращательные степени свободы атомов и молекул. Для возбуждения этих степеней свободы достаточно одного, двух соударений, поэтому ударную волну можно считать поверхностью, а следовательно можно воспользоваться соотношениями (5.18 – 5.21). Поскольку для совершенного газа:
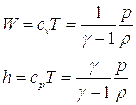
то из этих соотношений можно получить:

отсюда после замены плотности удельными объемами ![]() следует:
следует:
![]()
здесь ![]() - соответственно теплоемкости газа при постоянном объеме и постоянном давлении;
- соответственно теплоемкости газа при постоянном объеме и постоянном давлении; ![]() .
.
Это соотношение определяет в плоскости ![]() семейство кривых, которое можно построить, задавая значения двух параметров: начального давления
семейство кривых, которое можно построить, задавая значения двух параметров: начального давления ![]() и удельного объема
и удельного объема ![]() .
.
Ударная адиабата изображена на рис. 6.1. Эта кривая имеет вертикальную асимптоту, поскольку из предыдущей формулы следует, что отношение давлений неограниченно возрастает, если отношение плотностей принимает значение:
![]()
Следует подчеркнуть важное отличие ударной адиабаты от адиабаты Пуассона: вдоль одной и той же ударной адиабаты энтропия газа изменяется.
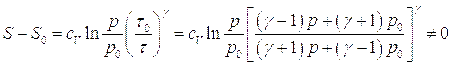
Энтропия в ударной волне терпит разрыв наряду с другими параметрами газа, причем в силу закона возрастания энтропии – энтропия газа, прошедшего через ударную волну должна быть больше его начальной энтропии. Последнее означает, что наличие ударных волн в газе, даже и не обладающем вязкостью и теплопроводностью ведет к необратимости движения, т.е. имеет место диссипация энергии. Следовательно, ударные волны представляют собой механизм, при котором происходит непосредственный переход видимого движения в тепловое.
Воспользуемся условием возрастания энтропии, т.е. будем считать, что ![]() , тогда из последнего соотношения получим:
, тогда из последнего соотношения получим: ![]() . Это означает, что не может быть ударной волны разрежения, поэтому участок адиабаты Гюгонио правее точки
. Это означает, что не может быть ударной волны разрежения, поэтому участок адиабаты Гюгонио правее точки ![]() на рис. 6.1 изображен пунктиром.
на рис. 6.1 изображен пунктиром.

Рис. 6.1
Последовательность адиабат ![]() на этом рисунке иллюстрирует процесс сжатия газа с помощью ударных волн, следующих одна за другой. Ход этих адиабат показывает, что невозможно, исходя из одного или того же начального состояния, прийти к одному конечному состоянию путем сжатия одной и несколькими ударными волнами. В отличие от этого адиабата Пуассона (PP – на рис. 6.1) может быть разбита на сколь угодно большее число участков, после реализации которых будет иметь место то же давление, что и при реализации исходного процесса. Последнее есть следствие того, что адиабата Пуассона зависит от одного параметра – энтропии, тогда как ударная адиабата – от двух.
на этом рисунке иллюстрирует процесс сжатия газа с помощью ударных волн, следующих одна за другой. Ход этих адиабат показывает, что невозможно, исходя из одного или того же начального состояния, прийти к одному конечному состоянию путем сжатия одной и несколькими ударными волнами. В отличие от этого адиабата Пуассона (PP – на рис. 6.1) может быть разбита на сколь угодно большее число участков, после реализации которых будет иметь место то же давление, что и при реализации исходного процесса. Последнее есть следствие того, что адиабата Пуассона зависит от одного параметра – энтропии, тогда как ударная адиабата – от двух.
Полученным результатом можно придать наглядный вид, если представить, что ударная волна распространяется с постоянной скоростью ![]() вдоль направления
вдоль направления ![]() . Воспользовавшись полученными выше формулами, нетрудно найти:
. Воспользовавшись полученными выше формулами, нетрудно найти:
 (6.1)
(6.1)
 (6.2)
(6.2)
 (6.3)
(6.3)
Здесь индексами ![]() помечены параметры газа, соответственно, до и после ударной волны, а
помечены параметры газа, соответственно, до и после ударной волны, а ![]() - есть отношение скорости распространения ударной волны к скорости звука в газе перед ударной волной, которое называют числом Маха ударной волны.
- есть отношение скорости распространения ударной волны к скорости звука в газе перед ударной волной, которое называют числом Маха ударной волны.
Нетрудно видеть, что при неограниченном возрастании скорости ударной волны, отношение плотностей стремится к предельному значению ![]() , которое для одноатомного газа равно примерно – 4, а для двухатомного – 6.
, которое для одноатомного газа равно примерно – 4, а для двухатомного – 6.
Если ударная волна встречает неподвижную стенку, расположенную перпендикулярную направлению ее распространения, то отношение скоростей отраженной и падающей ударных волн равно:
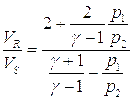
Воспользовавшись еще раз полученными выше соотношениями, связывающими параметрами до и после отраженной волны, а также формулами, связывающими параметры за падающей ударной волной с параметрами невозмущенного газа, можно найти:


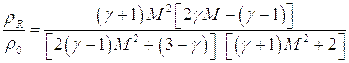
здесь индексом R – помечены параметры газа за отраженной волной, а индексом 0, как и прежде, параметры невозмущенного газа.
Подчеркнем, что приведенные формулы справедливы при ![]() , а это, в свою очередь, предполагает, что с газом, при переходе через ударную волну, не происходит физико-химических превращений. Однако такая идеализация не всегда соответствует действительности. С ростом числа Маха ударной волны за фронтом ударной волны происходит возбуждение внутренних степеней свободы молекул и атомов, а затем диссоциация молекул и ионизация атомов, следовательно, отношение теплоемкостей и молекулярный вес газа будут зависеть от температуры и давления. В этом случае для определения параметров среды за ударной волной целесообразно использовать непосредственно систему уравнений (5.18), предварительно вычислив внутреннюю энергию или энтальпию, как функции параметров среды. Вычисления становятся громоздкими, и это обстоятельство приводит к необходимости использования электронно-вычислительных машин (ЭВМ). Методика таких расчетов изложена, например, в [41,42].
, а это, в свою очередь, предполагает, что с газом, при переходе через ударную волну, не происходит физико-химических превращений. Однако такая идеализация не всегда соответствует действительности. С ростом числа Маха ударной волны за фронтом ударной волны происходит возбуждение внутренних степеней свободы молекул и атомов, а затем диссоциация молекул и ионизация атомов, следовательно, отношение теплоемкостей и молекулярный вес газа будут зависеть от температуры и давления. В этом случае для определения параметров среды за ударной волной целесообразно использовать непосредственно систему уравнений (5.18), предварительно вычислив внутреннюю энергию или энтальпию, как функции параметров среды. Вычисления становятся громоздкими, и это обстоятельство приводит к необходимости использования электронно-вычислительных машин (ЭВМ). Методика таких расчетов изложена, например, в [41,42].
При небольшом объеме расчетов можно использовать методику, которая состоит в следующем. Будем считать, что параметры среды перед ударной волной ![]() , а также скорость ударной волны известны. Запишем систему уравнений (5.18) в виде:
, а также скорость ударной волны известны. Запишем систему уравнений (5.18) в виде:
![]() (6.4)
(6.4)
![]() (6.5)
(6.5)
![]() (6.6)
(6.6)
где ![]() 0 и
0 и ![]() S – скорости среды соответственно до и после ударной волны, взятые в системе координат, связанной с ударной волной. Кроме того, будем считать, что уравнения состояния среды перед и за ударной волной могут быть записаны в такой форме:
S – скорости среды соответственно до и после ударной волны, взятые в системе координат, связанной с ударной волной. Кроме того, будем считать, что уравнения состояния среды перед и за ударной волной могут быть записаны в такой форме: ![]() а зависимости
а зависимости ![]() и
и ![]() - известны. Для решения этой системы уравнений воспользуемся методом последовательных приближений. Поскольку для сильных ударных волн
- известны. Для решения этой системы уравнений воспользуемся методом последовательных приближений. Поскольку для сильных ударных волн ![]() , то в первом приближении можно пренебречь в (6.4 – 6.6) членами, содержащими
, то в первом приближении можно пренебречь в (6.4 – 6.6) членами, содержащими ![]() . Тогда из (6.4):
. Тогда из (6.4):
![]() ,
,
что равносильно:
![]()
из (5.24):
![]()
что равносильно:
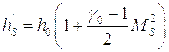
Далее, по известным значениям ![]() , с помощью функций
, с помощью функций ![]() и
и ![]() , можно найти
, можно найти ![]() , а затем
, а затем ![]() и скачок плотности
и скачок плотности  .
.
Из (6.4) следует:
![]()
Воспользовавшись этим соотношением, с помощью (6.5), получим во втором приближении:
![]()
Аналогично, с помощью (6.10):
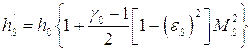
Поскольку функции ![]() и
и ![]() известны, то, зная
известны, то, зная ![]() и
и ![]() , можно найти
, можно найти ![]() , а затем и
, а затем и 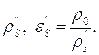
Далее могут быть сделаны третье, четвертое и т.д. приближения, но обычно второе приближение позволяет определить параметры за ударной волной с точностью, которая практически определяется той точностью, с которой известны функции ![]() ,
, ![]() , и точностью интерполяции при определении
, и точностью интерполяции при определении ![]() . Как показало сравнение результатов вычислений, проведенных по изложенной методике и с помощью ЭВМ по методике [41,42], значения параметров, вычисленных в обоих случаях для воздуха, в диапазоне скоростей ударной волны 5-8 км/сек, отличаются друг от друга не более чем на 1,5 %.
. Как показало сравнение результатов вычислений, проведенных по изложенной методике и с помощью ЭВМ по методике [41,42], значения параметров, вычисленных в обоих случаях для воздуха, в диапазоне скоростей ударной волны 5-8 км/сек, отличаются друг от друга не более чем на 1,5 %.
Схема расчета параметров за отраженными ударными волнами аналогична. В системе координат, связанной с отраженной ударной волной система уравнений (6.4-6.6), может быть записана в виде:
![]() (6.7)
(6.7)
![]() (6.8)
(6.8)
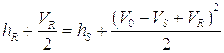 (6.9)
(6.9)
Как и прежде будем считать, что уравнения состояния среды, перед и за отраженной ударной волной, известны, а также известны зависимости ![]() и
и ![]() . С помощью (6.7-6.9), находим:
. С помощью (6.7-6.9), находим:
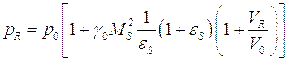 (6.10)
(6.10)
И, воспользовавшись (6.9):
 (6.11)
(6.11)
Однако эти соотношения непосредственно для расчета ![]() не могут быть использованы, поскольку содержат неизвестную величину
не могут быть использованы, поскольку содержат неизвестную величину ![]() . Воспользуемся, поэтому, методом последовательных приближений. В качестве исходного значения можно принять
. Воспользуемся, поэтому, методом последовательных приближений. В качестве исходного значения можно принять ![]() . Это значение можно найти, воспользовавшись формулой для отношения
. Это значение можно найти, воспользовавшись формулой для отношения ![]() , приведенной выше, если учесть, что при высоких температурах, значение
, приведенной выше, если учесть, что при высоких температурах, значение ![]() для двухатомного в исходном состоянии газа близко к 1,2 – 1,3. Например, в случае воздуха при температурах 6000 – 16000K и давлениях 1 – 150 атм., значения
для двухатомного в исходном состоянии газа близко к 1,2 – 1,3. Например, в случае воздуха при температурах 6000 – 16000K и давлениях 1 – 150 атм., значения ![]() лежат между 1,2 – 1,3. Выбор исходного значения
лежат между 1,2 – 1,3. Выбор исходного значения ![]() не является принципиальным; удачный выбор этого значения сводит к минимуму число последовательных приближений. Приняв
не является принципиальным; удачный выбор этого значения сводит к минимуму число последовательных приближений. Приняв 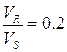 , получим, в первом приближении, из (6.10 – 6.11):
, получим, в первом приближении, из (6.10 – 6.11):
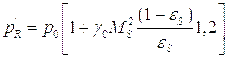
![]()
Затем, с помощью функций ![]() и
и ![]() , найдем первое приближение
, найдем первое приближение ![]() , а после этого и
, а после этого и ![]() . Подставив это значение в (6.9), получим первое приближение для
. Подставив это значение в (6.9), получим первое приближение для ![]()
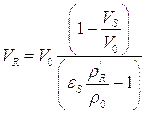
Воспользовавшись этим значением, можно, с помощью (6.10 – 6.11), найти значения ![]() во втором приближении, затем
во втором приближении, затем ![]() , а, следовательно, и второе приближение для
, а, следовательно, и второе приближение для ![]() . Обычно достаточно двух приближений, однако, при необходимости можно воспользоваться третьим, четвертым и т.д. приближениями.
. Обычно достаточно двух приближений, однако, при необходимости можно воспользоваться третьим, четвертым и т.д. приближениями.

Рис.6.2.
Сообщим в начальный момент поршню весьма малую скорость ![]() . Это приведет к возникновению в газе слабой волны уплотнения, которая будет распространяться слева направо со скоростью
. Это приведет к возникновению в газе слабой волны уплотнения, которая будет распространяться слева направо со скоростью  (рис. 6.2
(рис. 6.2 ![]() ). В любой момент времени газ перед фронтом волны уплотнения покоиться, тогда как между фронтом волны и поршнем газ приобретает скорость
). В любой момент времени газ перед фронтом волны уплотнения покоиться, тогда как между фронтом волны и поршнем газ приобретает скорость ![]() , а его плотность адиабатически возросла на величину
, а его плотность адиабатически возросла на величину ![]() . Увеличим скорость поршня еще на
. Увеличим скорость поршня еще на ![]() , по уплотненному газу от поршня к фронту начнет распространяться второе уплотнение (рис. 6.2
, по уплотненному газу от поршня к фронту начнет распространяться второе уплотнение (рис. 6.2 ![]() ). Повторяя этот процесс неоднократно, получим суперпозицию “
). Повторяя этот процесс неоднократно, получим суперпозицию “![]() ” волн уплотнения (рис. 6.2
” волн уплотнения (рис. 6.2 ![]() ), причем скорость газа между фронтом последней волны уплотнения и поршнем, составит
), причем скорость газа между фронтом последней волны уплотнения и поршнем, составит ![]() . Если приращения скорости
. Если приращения скорости ![]() и интервалы времени
и интервалы времени ![]() между двумя последующими приращениями скорости достаточно малы, а число уплотнений “
между двумя последующими приращениями скорости достаточно малы, а число уплотнений “![]() ” – достаточно велико, то по истечении конечного интервала времени t, получим практически непрерывное увеличение скорости от 0 до
” – достаточно велико, то по истечении конечного интервала времени t, получим практически непрерывное увеличение скорости от 0 до ![]() (рис. 6.2
(рис. 6.2 ![]() ). Скорость волны уплотнения тем больше, чем ближе волна к поршню, поскольку движется она по газу предварительно сжатому предыдущим уплотнением, а, следовательно, имеющим более высокую температуру, чем газ перед предыдущим уплотнением. Таким образом, в процессе движения каждый последующий слой догоняет двигающийся перед ним, поэтому в некоторый момент времени
). Скорость волны уплотнения тем больше, чем ближе волна к поршню, поскольку движется она по газу предварительно сжатому предыдущим уплотнением, а, следовательно, имеющим более высокую температуру, чем газ перед предыдущим уплотнением. Таким образом, в процессе движения каждый последующий слой догоняет двигающийся перед ним, поэтому в некоторый момент времени ![]() образуется крутой волной фронт (рис. 6.2 –
образуется крутой волной фронт (рис. 6.2 – ![]() ). В дальнейшем последующие уплотнения не могут обогнать предыдущие и распределение скоростей, показанное на рис. 6.2
). В дальнейшем последующие уплотнения не могут обогнать предыдущие и распределение скоростей, показанное на рис. 6.2 ![]() пунктиром, невозможно, т.к. в этом случае одному и тому же сечению трубы в данный момент соответствовало бы несколько значений скоростей газа. Возникает скачкообразное изменение скорости, соответствующее ударной волне. Проведенное рассмотрение позволяет сделать заключение, что в случае распространения волн уплотнения конечной амплитуды в отличие от распространения малых возмущений начальная форма распределения параметров в волне не сохраняется.
пунктиром, невозможно, т.к. в этом случае одному и тому же сечению трубы в данный момент соответствовало бы несколько значений скоростей газа. Возникает скачкообразное изменение скорости, соответствующее ударной волне. Проведенное рассмотрение позволяет сделать заключение, что в случае распространения волн уплотнения конечной амплитуды в отличие от распространения малых возмущений начальная форма распределения параметров в волне не сохраняется.
Определим место и время образования ударной волны перед поршнем. Эта задача, как и рассмотренная в следующем параграфе, является автомодельной и для нее справедливы уравнения (5.1). Справа от поршня в начальный момент и перед фронтом волны уплотнения нет источников возмущений, поэтому нет причин для распространения возмущений справа налево навстречу движению поршня вдоль ![]() – характеристик, следовательно, можно считать, что
– характеристик, следовательно, можно считать, что ![]() – инвариант Римана остается постоянным во всей области справа от поршня. Преобразуем
– инвариант Римана остается постоянным во всей области справа от поршня. Преобразуем ![]() – инвариант:
– инвариант:
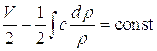
считая процесс распространения звука адиабатическим, т.е.
![]()
![]()
поделив почленно эти уравнения:
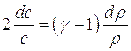
Воспользовавшись этим соотношением, заменим в ![]() – инварианте
– инварианте ![]() , после интегрирования получим:
, после интегрирования получим:

Полагая, что при ![]() ,
, ![]() , найдем, что
, найдем, что 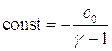 , следовательно:
, следовательно:
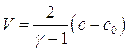
![]()
![]()
Отсюда следует, что для волн распространяющихся вдоль ![]() – характеристик, чем больше скорость
– характеристик, чем больше скорость ![]() возмущенного движения газа тем больше, как скорость абсолютного распространения волны:
возмущенного движения газа тем больше, как скорость абсолютного распространения волны: ![]() , так и относительного распространения волны
, так и относительного распространения волны ![]() . Большим значением скорости “
. Большим значением скорости “![]() ” соответствует и большие значения плотности и давления, а это означает, чем больше интенсивность переносимого возмущения, тем больше и скорость распространения возмущения. Следовательно, форма распределения конечного возмущения, в отличие от малых возмущений, при распространении в газе не сохраняется. В этом состоит основное отличие распространения возмущений конечной интенсивности от распространения звуковых волн.
” соответствует и большие значения плотности и давления, а это означает, чем больше интенсивность переносимого возмущения, тем больше и скорость распространения возмущения. Следовательно, форма распределения конечного возмущения, в отличие от малых возмущений, при распространении в газе не сохраняется. В этом состоит основное отличие распространения возмущений конечной интенсивности от распространения звуковых волн.
Поскольку вдоль характеристик сохраняется скорость газа – ![]() и скорость звука –
и скорость звука – ![]() , то семейство
, то семейство ![]() – характеристик, отвечающих условию
– характеристик, отвечающих условию
![]()
будет представлять собой совокупность прямых линий. Семейство ![]() – характеристик, отвечающих ускоренному движению поршня, изображено на рис. 6.3.
– характеристик, отвечающих ускоренному движению поршня, изображено на рис. 6.3.
Предположим, что в некоторый момент времени ![]() в сжатом перед поршнем газе имеет место распределение скоростей, которое можно описать функцией
в сжатом перед поршнем газе имеет место распределение скоростей, которое можно описать функцией ![]() , убывающей в направлении движения поршня. В последующий момент времени
, убывающей в направлении движения поршня. В последующий момент времени ![]() распределение скорости приобретает более резкий спад, т.к. точки кривой
распределение скорости приобретает более резкий спад, т.к. точки кривой ![]() , которые можно рассматривать как волны сжатия, переместятся вдоль оси Ox на расстояния:
, которые можно рассматривать как волны сжатия, переместятся вдоль оси Ox на расстояния:
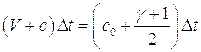
т.е. тем больше, чем больше ординаты кривой ![]() . Наклон кривой будет возрастать с течением времени пока наконец не приобретет форму ступеньки, показанную на рис. 6.2
. Наклон кривой будет возрастать с течением времени пока наконец не приобретет форму ступеньки, показанную на рис. 6.2 ![]() . В этот момент времени
. В этот момент времени ![]() в одной из точек кривой
в одной из точек кривой ![]() , касательная к ней станет перпендикулярной оси ОX, т.е.
, касательная к ней станет перпендикулярной оси ОX, т.е. ![]()
Поскольку кривая распределения скоростей в момент времени ![]() :
: ![]() получается из кривой
получается из кривой ![]() параллельным переносом ординат на расстояние, указанное выше, то можно написать:
параллельным переносом ординат на расстояние, указанное выше, то можно написать:
![]()
где 
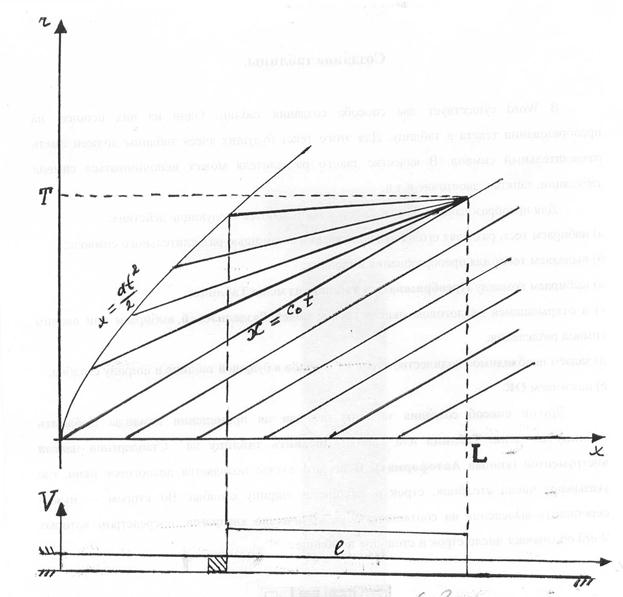
Рис.6.3.
Продифференцируем по ![]() написанное уравнение:
написанное уравнение:
![]()
Поскольку
![]() ,
,
то
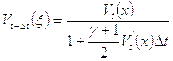
Обозначим ![]() абсциссу точки, в которой кривая изменяется скачкообразно, т.е. производная обращается в бесконечность. Поскольку
абсциссу точки, в которой кривая изменяется скачкообразно, т.е. производная обращается в бесконечность. Поскольку ![]() есть величина конечная, то на основании последнего равенства можно утверждать, что
есть величина конечная, то на основании последнего равенства можно утверждать, что
![]()
или
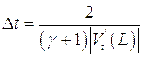
Полагая ![]() и считая
и считая ![]() , найдем, что
, найдем, что ![]() . Поскольку
. Поскольку ![]() есть фактическое ускорение поршня –
есть фактическое ускорение поршня – ![]() , т.к. в начальный момент фронт волны сжатия практически совпадает с торцевой поверхностью поршня, то
, т.к. в начальный момент фронт волны сжатия практически совпадает с торцевой поверхностью поршня, то ![]() есть скорость распространения волны по невозмущенному газу, т.е. –
есть скорость распространения волны по невозмущенному газу, т.е. – ![]() . Таким образом,
. Таким образом,
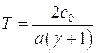
Расстояние до места образования ударной волны, как это следует из рис. 6.3, ![]() , т.е.
, т.е.
![]()
Длина области ударно нагретого газа:
![]()
Влево от поршня по первоначально покоящемуся газу вдоль ![]() – характеристик будут распространяться волны разрежения, т.е. плотность в направлении обратном движению поршня будет убывать.
– характеристик будут распространяться волны разрежения, т.е. плотность в направлении обратном движению поршня будет убывать.
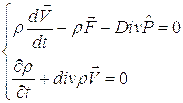
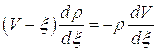 (6.12)
(6.12) (6.13)
(6.13)
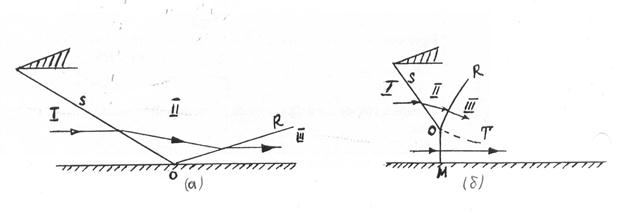
 , то в конечном счете эта волна сжатия превратится в ударную волну. Линия ударной волны на рис.(6.4а) обозначена ОА, а линия раздела газов высокого и низкого давлений – ОВ. Между этими границами располагается область с постоянными значениями термодинамических параметров. Это утверждение основано на том, что увеличение значений этих параметров в направлении Ох привело бык превращению волны сжатия в ударную волну, а этот факт уже имеет место. Уменьшение значений параметров в направлении оси Ох свидетельствовало бы о существовании ударной волны разрежения, что невозможно.
, то в конечном счете эта волна сжатия превратится в ударную волну. Линия ударной волны на рис.(6.4а) обозначена ОА, а линия раздела газов высокого и низкого давлений – ОВ. Между этими границами располагается область с постоянными значениями термодинамических параметров. Это утверждение основано на том, что увеличение значений этих параметров в направлении Ох привело бык превращению волны сжатия в ударную волну, а этот факт уже имеет место. Уменьшение значений параметров в направлении оси Ох свидетельствовало бы о существовании ударной волны разрежения, что невозможно.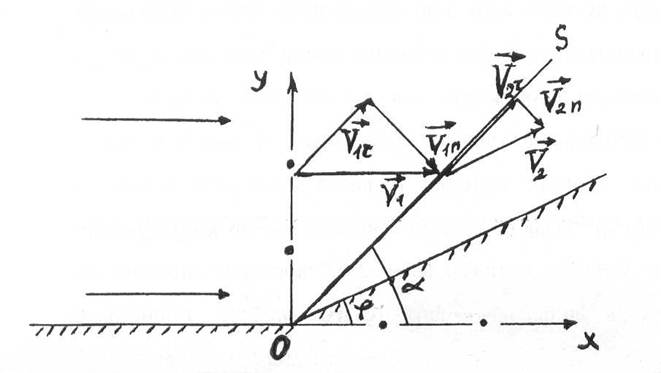
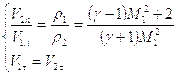
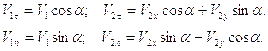
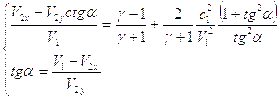
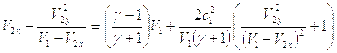

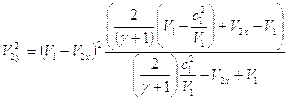


Рис. 6.6.
На рисунке 6.6 приведен вид строфоиды. Она пересекает ось абсцисс в точках Р и Q, которые соответствуют значениям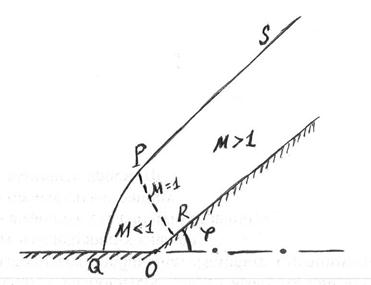
Рис. 6.7
Течение за такой ударной волной является вихревым. Непосредственно за точкой Q параметры газа за отсоединенной ударной волной близки параметрам за прямым скачком, далее течение становится похожим на течение за сильным скачком, а затем аналогичным течению за слабым косым скачком. Вместе с тем течение переходит от до звукового к сверхзвуковому. Аналогично изложенному, при обтекании клина возникают отсоединенный или присоединенный скачки уплотнения, в соответствии с тем, превышает или нет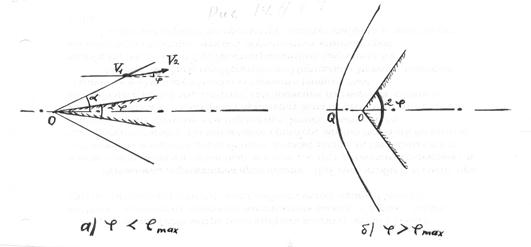

![]() →
→ ![]()
- если ударная волна в одном газе встречает другой газ с большей скоростью звука, то на поверхности разрыва возникают прошедшая и отраженная ударные волны.
![]() →
→ ![]()
- если во второй среде скорость звука меньше, то возникают две возможности:
а) если величина ![]() во второй среде меньше или если ударная волна достаточно слаба, то проходит ударная волна и отражается волна разрежения:
во второй среде меньше или если ударная волна достаточно слаба, то проходит ударная волна и отражается волна разрежения:
![]() →
→![]()
б) если величина ![]() во второй среде больше и ударная волна достаточно сильна, проходит волна разрежения и отражается ударная волна
во второй среде больше и ударная волна достаточно сильна, проходит волна разрежения и отражается ударная волна
![]() →
→![]()
-столкновение двух волн разрежения
![]() →
→![]()
-столкновение волны разрежения с зоной большей скорости звука
![]() →
→![]()
-столкновение волны разрежения с зоной большей скорости звука
![]() →
→![]()
Взаимодействие ![]() производит волну сжатия, в которой, в конце концов, образуется ударная волна.
производит волну сжатия, в которой, в конце концов, образуется ударная волна.
Если ударная волна перегоняет волну разрежения или волна разрежения перегоняет ударную волну (в том случае, когда интенсивность обгоняющей волны значительно больше обгоняемой), то
![]() →
→![]()
![]() →
→![]()
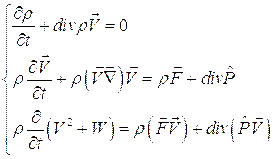 (6.16)
(6.16)
 |
 |