ГЛАВА VII.
Экспериментальное изучение состояния сред за мощными ударными волнами.
Распространение возмущений повышенной плотности в газах ведет к возникновению ударных разрывов, по обе стороны которых параметры среды связаны между собой законами сохранения на ударном разрыве (5.18). За ударной волной скачком возрастает температура среды, причем с ростом скорости распространения волны значения температуры достигают таких величин, что за фронтом волны начинаются физико-химические превращения вещества, которые существенно влияют на процессы распространения ударных волн, взаимодействия их между собой и с препятствиями, весьма важным становится процесс переноса энергии излучением; теоретическое описание поведения среды сильно осложняется и становится, как это показано выше, практически неразрешимой задачей. Необходимы экспериментальные сведения о поведении сплошных сред в таких условиях. Наиболее перспективным источником сведений о поведении и свойствах неизотермических сжимаемых сред, является ударная труба.
§1. Эффекты, сопровождающие распространение ударных волн в каналах.
Простейшая ударная труба представляет собой канал цилиндрического сечения, разделенный тонкой металлической диафрагмой. Давление в одном из отсеков значительно больше, чем во втором. На диафрагме сделаны радиальные насечки с таким расчетом, чтобы разрыв диафрагмы происходил при повышении давления в первом отсеке до определенного уровня. После разрыва диафрагмы газ из отсека высокого давления устремляется в отсек низкого давления, перед ним формируется ударная волна. Между ударной волной и областью контакта газов отсеков высокого и низкого давления образуется область ударно нагретого газа. Если известна скорость распространения ударной волны, состав, температура и давление газа перед ней то, как показано в §1 гл.VI, уравнения (5.18) позволяют определить термодинамические параметры непосредственно за фронтом ударной волны. Вместе с тем целый ряд эффектов осложняет описание состояния среды за ударной волной.
Разрушение диафрагмы происходит не мгновенно. По данным [46-49] время раскрытия, зависит от материала диафрагмы, величины высокого давления и других условий опыта и колеблется от 100 до 1000 мкс. Картина течения во время разрыва диафрагмы развивается таким образом: после разрушения центральной части диафрагмы начинается истечение газа. Перед истекающим газом формируется ударная волна. Около диафрагмы возникает разрыв, напоминающий по форме язык пламени и опирающейся на края отверстия в диафрагме, аналогичный описанному в §4 гл.V. Скорость перемещения этого разрыва сначала быстро растет, затем уменьшается, скачок останавливается и распадается на два возмущения, одно из которых распространяется по потоку, а другое - против него. Возмущения, вызванные истекающей струей, отражаются от стенок канала, образуя характерную сетку прямых, и создают неоднородности в структуре потока. Поверхность контактной области, обращенная в сторону движения, приобретает сложную форму, напоминающую в первом приближении колоколообразную [50]. Газы, находящиеся по разные стороны от контактной области перемешиваются, что находит свое подтверждение в экспериментах по поглощению линий хрома, результаты которых изложены в [51]. Наличие области смешения влечет за собой неоднородность потока. Создание схемы расчета параметров среды за ударной волной полностью учитывающей изложенную картину течения весьма трудная задача, осложненная тем, что имеющиеся экспериментальные данные относятся в основном к небольшим числам Маха (М<10). Обзор результатов и обсуждение влияния конечного времени раскрытия диафрагмы выполнены в [53,54].
Серьезно осложняет состояние среды между контактной областью и ударной волной вязкость, которая приводит к образованию слоя около стенки канала ударной трубы, обусловленного вязкостью среды. Образование такого слоя ведет к появлению слабых волн сжатия, которые вызывают уменьшение скорости ударной волны. Кроме того, газ из этого слоя вытесняется в контактную область, что влечет за собой ее ускорение, а, следовательно, и уменьшение расстояния между ней и ударной волной. Необходимо отметить, что наличие такого слоя приведет к дополнительной неоднородности потока, как перпендикулярно направлению потока, так и вдоль по потоку. Наиболее полно эти эффекты, в предположении теории пограничного слоя Прандтля рассмотрены в [54-58], причем принятая в этих работах идеализация дополнительно серьезно ограничивает область применения и достоверность результатов. Предполагается: I- участок формирования и ускорения ударной волны отсутствует, ударная волна сразу возникает перед плоской контактной поверхностью и далее распространяется с постоянной скоростью, 2-вне пограничного слоя течение считается потенциальным, подверженным малым возмущениям, 3-толщина пограничного слоя мала по сравнению с поперечными размерами ударной трубы, 4- стенка является источником возмущений, дающим только продольные волны, 5-среда до и после ударной волны остается идеальной с постоянным значением отношения теплоемкостей, для вязкости справедлив закон Сазерленда, 6-ширина волны разрежения за контактной областью пренебрежимо мала. В этих предположениях проведено рассмотрение как ламинарного, так и турбулентного слоя, развивающегося за ударной волной. В [53] исходя из экспериментальных данных положено, что критическим значением числа Рейнольдса, при котором происходит переход ламинарного слоя в турбулентный, является 1÷3·106 для ударных волн с M≤9, для более сильных волн 5·107. Сравнение, приведенное в [53], говорит об удовлетворительном согласии до чисел M≤10 вычисленных согласно [57] и измеренных расстояний между ударной волной и контактной поверхностью. Указанное согласие не является удивительным, т.к. по-видимому, газ из неоднородной области, возникшей при формировании ударной волны и на участке ее ускорения, к моменту регистрации находился уже за внешней поверхностью контактной области. В [58] для случая ламинарного пограничного слоя в предположении, что роль слоя сводится к уменьшению сечения канала, в котором распространяется ударная волна, найдено возрастание температуры, плотности и давления в направлении от ударной волны и контактной поверхности соответственно на 8, 12 и 20%. Экспериментальные исследования, результаты которых изложены в [53], позволили установить возрастание скорости потока у контактной области, находящиеся в согласии с [58]. Измерения температуры за падающими ударными волнами [60] свидетельствуют о том, что значения температуры непосредственно за ударной волной (при числах M≤10) совпадают в пределах точности эксперимента с рассчитанными по законам сохранения, однако в отличие от [58] температура не возрастает к контактной области, а уменьшается. В [61] установлено, что значения давления за ударными волнами в воздухе отвечают расчетным вплоть до M≤17. Приведенные здесь два экспериментальных значения давления для чисел M≈37 лежат существенно ниже расчетной кривой, что лишь подчеркивает необходимость измерения параметров плазмы, за мощными ударными волнами.
Для мощных ударных волн становится весьма существенным еще один фактор - излучение. Этот фактор приводит к тому, что в уравнении энергии нельзя не учитывать источники и стоки энергии, поскольку излучение ведет к охлаждению среды, а поглощение дает обратный эффект. Система уравнений, учитывающая перенос энергии излучением является интегро-дифференциальной и решение ее найдено лишь для отдельных случаев, в частности, для одномерных течений и близких к ним. В [62-64] изучалась роль охлаждения излучением аргоновой плазмы за ударными волнами. Укажем, что в расчетах [63-64] рассматривались стационарные ударные волны в ударной трубе, влияние участка формирования и ускорения ударной волны, а также влияние пограничного слоя на параметры потока за ударной волной, не учитывалось. Из [63] следует, что охлаждение за счет радиации приводит к тому, что температура за ударной волной в аргоне при М=17 и начальном давлении 10 мм рт. ст. уменьшается на длине в 10 см примерно на 20%. В [64] получен темп изменения температуры меньше, чем в [63], т.к. в [64] не учитывался вклад линий аргона. Отметим, что расчеты [63] находятся в удовлетворительном согласии с экспериментальными данными [62]. Аналогичные результаты получены в [65] при изучении ударных волн в аргоне в электроразрядной ударной трубе (с диафрагмой). Необходимо указать, что излучение, проникающее в область перед ударной волной вызывает предварительную ионизацию газа за счет фотоэффекта (см. напр. [66]).
Для более мощных ударных волн становится существенным другой эффект: излучение, идущее от плазмы за ударной волной, нагревает газ перед волной, что, естественно, влечет за собой изменение параметров за ней. Это обстоятельство становится существенным при весьма больших скоростях ударных волн. Так, например, согласно [67] воздух нормальной плотности прогревается перед волной до ~4000К при температуре за волной 50000К. Далее температура перед волной (в приближении лучистой теплопроводности) растет еще быстрее, и при температуре за ударной волной около 300000К становится примерно ей равной. Учет деталей приводит к тому, что на кривой температуры все еще сохраняется скачок, обусловленным ударным сжатием.
Краткое рассмотрение эффектов, имеющих место за ударной волной, указывает на необходимость учета неодномерности потока при рассмотрении мощных ударных волн в каналах, изменения физико-химических свойств вещества, наличия источников излучения и поглощения, т.е. решения уравнений (1.5;1.6;1.7) с учетом гипотезы (2.3) в полном объеме, при этом должны быть известны термодинамические функции и оптические свойства сред в широком диапазоне температур и давлений. Теоретическое рассмотрение газодинамических задач в этих условиях становится исключительно громоздким и сопряжено с практически неопределенными математическими трудностями. Это обстоятельство диктует настоятельную необходимость экспериментальных исследований состояния сплошных сред за ударными волнами, распространяющимися с гиперзвуковыми скоростями. Изложению результатов таких экспериментов предпошлем описание ударных труб, позволяющих получать мощные ударные волны.
§2. Принципы действия мощных ударных труб.
Проведем расчет параметров сплошной среды в ударной трубе, исходя из предположения, что после разрыва диафрагмы газы, находившиеся в отсеках высокого и низкого давлений, разделены непроницаемой контактной поверхностью и поэтому не перемешиваются. Будем считать, что 1 – газ отсеке высокого давления идеальный, причем показатель адиабаты Пуассона после разрыва диафрагмы остается неизменными, 2 – перед контактной поверхностью мгновенно формируется ударная волна, которая распространяется затем с постоянной скоростью, 3 – влиянием вязкости, теплопроводности, а также излучением и поглощением среды можно пренебречь, т.е. течение можно полагать одномерным.
На рис. 7.1 изображена x-t диаграмма процессов, происходящих в ударной трубе в этом случае и распределение термодинамических параметров газа вдоль по трубе; здесь обозначены: индексом m – параметры газа высокого давления, индексом w – параметры газа высокого давления, который испытывает расширение в простой изэнтропической волне разрежения, индексом s – параметры ударного газа, находящегося между ударной волной и контактной поверхностью, индексом о – параметры невозмущенного газа в отсеке низкого давления.
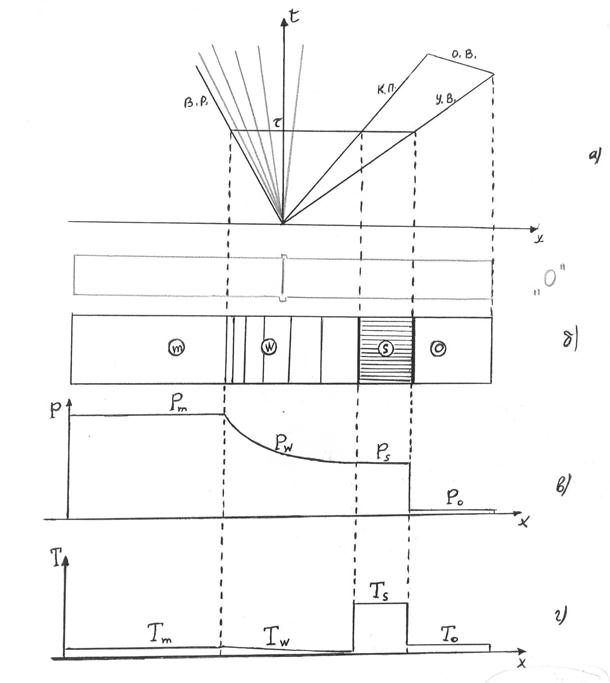
Рис. 7.1.
Будем считать газ в отсеке высокого давления совершенным, тогда в случае адиабатического расширения справедливо:

откуда:
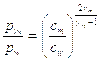
здесь индексами 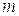 и
и  отмечены параметры газов в невозмущенной части газа высокого давления и в испытывающей адиабатическое расширение.
отмечены параметры газов в невозмущенной части газа высокого давления и в испытывающей адиабатическое расширение.
Волны разрежения в отсеке высокого давления можно рассматривать, как простые волны конечной амплитуды, следовательно, для них справедливы соотношения (5.8), причем согласно § 1 гл. V для идеального газа:

что позволяет написать:

Невозмущенный газ в отсеке высокого давления покоится, 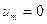 . Отметим также, что вблизи контактной поверхности давление и скорость среды непрерывны, т.е.
. Отметим также, что вблизи контактной поверхности давление и скорость среды непрерывны, т.е.
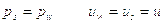
где 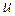 – скорость спутного потока.
– скорость спутного потока.
Поэтому

и формула для отношения давлений преобразуется к виду:
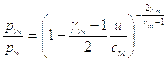
С другой стороны согласно (6.1)
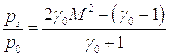
где  - число Маха ударной волны.
- число Маха ударной волны.
Из двух последних соотношений найдем:
 (7.1)
(7.1)
Скорость движения возмущенного газа за ударной волной, которое можно считать спутным потоком газа за ударной волной:

Для определения скорости u спутного потока воспользуемся формулой Прандтля (5.26) в виде:

Исключая, с помощью предыдущего соотношения 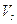 , получим:
, получим:

Воспользовавшись (5.25) можно записать:
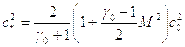
Подставляя в предыдущую формулу, получим:

Это соотношение позволяет уравнению (7.1) придать вид:
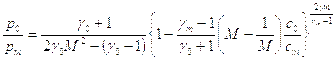
Обычно давление в отсеке низкого давления в ударных трубах составляет несколько миллиметров ртутного столба, тогда как в отсеке высокого давления – несколько атмосфер и более, поэтому  и
и 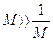 . В этом случае выражение в фигурных скобках должно быть близко к нулю, откуда
. В этом случае выражение в фигурных скобках должно быть близко к нулю, откуда
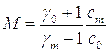 (7.2)
(7.2)
Из (7.2) следует, что при максимально возможном перепаде давлений для повышения скорости ударной волны необходимо увеличивать скорость звука в отсеке высокого давления, оставляя γ при этом возможно меньшим. С этой точки зрения наиболее эффективными является применение в камере высокого давления водорода. Дальнейшее увеличение скорости звука в газе камеры высокого давления возможно за счет повышения его температуры. В лабораторных условиях могут быть использованы как внешний, так и внутренний подогрев с помощью нагревательных элементов, а также внутренний подогрев с помощью электрического разряда, химической реакции или ударных волн. Внутренний подогрев с помощью твердых нагревательных элементов предпочтительнее, чем внешний, т.к. при внутреннем подогреве стенки могут находиться при более низкой температуре, чем газ. Кроме того, в этом случае стенки можно покрыть теплоизолирующим материалом и тем самым повысить эффективность подогрева. Однако применение твердых нагревательных элементов делает экспериментальную установку весьма громоздкой, поэтому обычно используется внутренний подогрев с помощью электрического разряда или химической реакции. При подогреве электрическим разрядом в камере высокого давления используется обычно гелий, т.к. в этом случае не расходуется энергия на диссоциацию и ионизацию, поскольку гелий одноатомный газ, обладающий самым высоким потенциалом ионизации. Ограниченные возможности накопления электроэнергии в обычных лабораторных условиях (~106 дж) не позволяют нагреть большие порции газа, поэтому нагрев с помощью электрического разряда используется обычно для получения ударных волн при низких начальных давлениях (1 мм рт. ст. и менее). Химический способ подогрева водорода имеет тот недостаток, что в результате реакции молекулярный вес становиться больше молекулярного веса водорода. Однако при отношении молярных долей 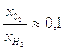 можно получить выигрыш в скорости звука по сравнению с водородом согласно [68] примерно в 1,7 раза. Ту часть водорода, которая не участвует в реакции (~ 70 %), можно заменить гелием. Кислородо-водородо-геливая смесь (КВГС): 1O2 + 2Н2 +7Не практически столь же эффективно повышает скорость ударной волны, как и смесь 1O2 + 9Н2 [61], а соображения безопасности делают более предпочтительным применение КВГС. Согласно [61] наибольшие скорости ударной волны получаются в том случае, когда давление, при котором разрушается диафрагма, примерно в два раза меньше, чем давление, развивающиеся при полном сгорании КВГС в замкнутом сосуде.
можно получить выигрыш в скорости звука по сравнению с водородом согласно [68] примерно в 1,7 раза. Ту часть водорода, которая не участвует в реакции (~ 70 %), можно заменить гелием. Кислородо-водородо-геливая смесь (КВГС): 1O2 + 2Н2 +7Не практически столь же эффективно повышает скорость ударной волны, как и смесь 1O2 + 9Н2 [61], а соображения безопасности делают более предпочтительным применение КВГС. Согласно [61] наибольшие скорости ударной волны получаются в том случае, когда давление, при котором разрушается диафрагма, примерно в два раза меньше, чем давление, развивающиеся при полном сгорании КВГС в замкнутом сосуде.
Для того, чтобы в качестве толкающего использовать газ, нагретый ударной волной, между камерами высокого и низкого давления устанавливают промежуточную камеру, заполняемую гелием или водородом при давлении от нескольких десятых долей атмосферы до нескольких атмосфер. После разрыва первой диафрагмы, отделяющей камеру высокого давления от промежуточной, по газу в промежуточной камере распространяется ударная волна, встречающая на своем пути вторую диафрагму. Далее в зависимости от прочности этой диафрагмы могут иметь место три случая:
а) – вторая диафрагма имеет столь малую прочность, что разрушается тотчас же после соприкосновения с ударной волной. Газ расширяется в нестационарной волне разрежения, перед которой формируется ударная волна, распространяющаяся по газу в камере низкого давления.
б) – вторая диафрагма обладает такой прочностью, что разрушение наступает после встречи отраженной от нее ударной волны с контактной поверхностью и последующего перемешивания газов.
Этот случай является нежелательным, т.к. он по существу не отличается от одно-диафрагменного режима.
в) – вторая диафрагма обладает “умеренной” прочностью, т.е. такой, что ее разрушение происходит после отражения от нее ударной волны, но до момента встречи отраженной волны с контактной поверхностью. Расчет [69] показывает, что последний случай несколько предпочтительнее первого.
Таким образом, прочность второй диаграммы, так же как и прочность первой, должна быть оптимальной. Давление в промежуточной камере, как это следует из [69], тоже должно быть оптимальным. Необходимо подчеркнуть, что изложенное здесь рассмотрение исходит из простейшей картины течения и не учитывает эффектов, о которых шла речь выше, однако качественно изложенная схема, по-видимому, отражает реальные процессы. Использование промежуточной камеры в оптимальном режиме в случае комбинации гелий-воздух позволило согласно [70] увеличить скорость ударной волны на 30 %. Применение второй, третьей и т.д. промежуточных камер дает существенно меньший эффект, ведет к громоздкости эксперимента, увеличению расхода газа и т.д. и поэтому обычно не практикуется. Для дальнейшего увеличения скорости можно воспользоваться сужением сечения в промежуточной камере. Это приведет к увеличению скорости ударной волны в этой камере, а следовательно и к форсированию параметров в исследуемом газе. Для генерации мощных ударных волн можно воспользоваться детонацией конденсированного взрывчатого вещества [70-72]. Скорость истечения продуктов детонации в разреженную среду составляет, согласно [73], 17 км/сек. В простейшей схеме такой ударной трубы [74,75] используется разлет продуктов детонационной волны взрывчатого вещества (ВВ) непосредственно в исследуемый газ; диафрагма между зарядом ВВ и исследуемым газом не ставится. Процессы формирования и ускорения ударных волн в каналах в этом случае по существу не изучены. Обычно фронт свечения отождествляется с фронтом ударной волны, а скорость распространения этого фронта отождествляют со скоростью ударной волны. Используя самосвечение, авторы [75] нашли, что плоские ударные волны образуются при начальном давлении 1 мм рт. ст. и выше. При давлении ниже 1 мм рт. ст. продукты детонации разлетаются в исследуемом газе в виде отдельных струй. Размеры ударно нагретой области отвечают расчетам согласно [74,75].
В [75] с помощью ВВ получена скорость ударной волны 10 км/с в воздухе при начальном давлении 1 мм рт. ст., а в [74] сообщается о скорости 17,5 км/с в аргоне ( в последнем случае скорость измерялась на расстояние около 10 калибров от поверхности заряда ВВ). Серьезным недостатком ударных труб, использующих ВВ, является полное или частичное разрушение ударной трубы во время опыта. Это влечет за собой создание специальных помещений, приводит к громоздкости и удорожанию экспериментов. Весьма эффективным средством повышения скорости ударной волны является комбинирование способов, упомянутых выше. Так авторы [75] установив между зарядом ВВ и камерой низкого давления промежуточную камеру с гелием, сужающуюся в направлении распространения волны, получили скорость ударной волны в воздухе до 18,3 км/с (при начальном давлении 1 мм рт.ст). В устройстве, описанном в [77], заряд ВВ, позволяющий получить плоский фронт детонационной волны, после взрыва ускорял металлическую пластинку, которая двигалась в заполненной газом камере, имеющей форму сферического сегмента. В вершине сегмента имелось отверстие закрытое тонкой (8 мкм) лавсановой диафрагмой, за которым находилась трубка, заполненная исследуемым газом. В этой трубке диаметром 5 мм были получены скорости ударной волны в воздухе около 60 км/с, в водороде до 90 км/с. Следует отметить существенное падение скорости по длине трубки: на длине около 60 калибров скорость падает вдвое, тогда как в ударной трубке, использующей КВГС [61], на длине 100 калибров уменьшение скорости составляет 20 %. Другим недостатком устройства, описанного в [76], является весьма малый диаметр трубки. Согласно [57] размеры ударно нагретой области пропорциональны квадрату диаметра, т.е. в данном случае длина ударно нагретой области примерно на два порядка меньше, чем в обычных ударных трубах.
Весьма высокие скорости плазменных образований получены с помощью электромагнитных ударных труб (см. напр. [66,77]). Эти трубы состоят из разрядной камеры и цилиндрического канала, в котором движется плазма. Применяются разрядные камеры трех типов: 1 - цилиндр, расположенный перпендикулярно каналу: разряд происходит по оси цилиндра, обратный провод располагается по его образующей; 2- конус, в вершине которого расположен один электрод, а в основании второй, имеющий форму кольца; 3- два коаксиальных цилиндра. Омический нагрев за счет мощного импульса тока приводит к резкому повышению давления и температуры в разрядной камере. Кроме того, возникшее магнитное поле взаимодействует с током в разрядной камере и создает тем самым лоренцеву силу, которая дополнительно ускоряет плазму в канале. Отметим, что ускорение, обусловленное магнитным полем, как правило, существенно больше ускорения за счет повышения давления вследствие омического нагрева. Условия образования и движения "поршня" в канале в этом случае существенно отличаются от рассмотренных выше. Идеализированная схема процессов в электромагнитной ударной трубе обычно сводится к модели "гидродинамического" или "магнитного" поршня. Схема "гидродинамического поршня" предполагает, что контактная поверхность отделяет область ударно нагретого газа от "толкающей" плазмы, которая нагрета равномерно и к которой линейно со временем подводится энергия. В основу модели "магнитного поршня" положено представление о том, что контактная поверхность представляет собой токовый слой, к которому приложена лоренцева сила. Условность этих схем очевидна. Как показали исследования [[77,78]], в электромагнитных трубах область ударно нагретой плазмы, параметры которой отвечают уравнениям (5.18), образуется далеко не всегда. Интерферометрические исследования в водороде [79] с помощью электромагнитной трубу первого типа привели к следующим результатам: при начальных давлениях 2,5 + 10 мм рт. ст. и при числах. Маха ударной волны меньших 10 фронт ударной волны не виден, а при числах Маха больше 20 "толкающая плазма" догоняет фронт. Необходимо упомянуть, что в [77] установлено отставание фронта свечения от фронта ударной волны. Это заставляет относиться с большей осторожностью к выводам работ где фронт свечения отождествляется с фронтом ударной волны. Весьма существенным недостатком электромагнитных ударных труб является существенное уменьшение скорости ударной волна при распространении ее вдоль камеры низкого давления при начальных давлениях выше 0,1 мм рт. ст. [77], что может обусловить неоднородность параметров плазмы за ударной волной.
Таким образом, проведенное рассмотрение заставляет отдать предпочтение при выборе способа получения мощных ударных волн - ударным трубам, использующим в камере высокого давления КВГС и снабженным промежуточной камерой, наполненной гелием или водородом.
Большой интерес представляют исследования состояния среды за отраженными ударными волнами. Отраженная ударная волна практически мгновенно возникает у торца ударной трубы, участок формирования и ускорения по существу отсутствует, поэтому распространение отраженной волны в системе координат, связанной с торцом и распространение волны перед равномерно движущимся поршнем аналогично. Однако необходимо иметь в виду, что распространение отраженной волны осложнено наличием пограничного слоя, развившегося за падающей волной.
§3. Описание экспериментальных установок и методики измерения скорости ударных волн.
В соответствии с анализом, проведенным в §2, в качестве инструмента для получения мощных ударных волн были использованы одно- и двух диафрагменные ударные трубы, в камерах высокого давления которых применялась КВГС.
Давление КВГС в камерах как одно-, так и двух диафрагменных ударных труб могло достигать 50 атм. При сгорании этой смеси в замкнутом объеме давление возрастает примерно на порядок, следовательно для камер высокого давления необходимы трубы, обладающие высокой прочностью. Использовались два варианта камер высокого давления: 1) – труба из стали с внутренним диаметром 3 см и внешним - 6 см, длинною около 150 см с хромированной внутренней поверхностью, 2) – труба из нержавеющей стали с внутренним диаметром 10 см, внешним – 20 см, длиною 250 см с электрополированной внутренней поверхностью. После разрыва диафрагмы концы ее лепестков приобретают скорость, порядка 100 м/сек. При ударе лепестков диафрагмы о стенки ударной трубы последние испытывают весьма высокие нагрузки, поэтому промежуточная камера и первая секция камеры низкого давления изготавливалась из таких труб, что и камеры высокого давления. Последующие секции камер низкого давления имели различные сечения и размеры каналов: 1 – квадрат со сторонами 2,7 см, 2 – квадрат со сторонами 3 см, 3 – круг диаметром 3 см, 4 – круг диаметром 10 см. Секции типа 1 – 3 использовались совместно с камерами высокого давления с внутренним диаметром 3 см, типа 4 – с камерами диаметром 10 см. Между диафрагмой и секцией типа 1 устанавливалась секция длиною 15 см, форма сечения внутреннего канала которой изменялась в направлении движения газа от круглого (диаметром 3 см) к квадратному (со стороной 2,7 см). Между диафрагмой и секцией типа 2 устанавливалась сначала секция типа 3, затем секция длиною 30 см, форма сечения внутреннего канала которой плавно изменялась от круглого диаметром 3 см к квадратному со стороной 3 см. В двух вариантах ударных труб предусматривались внутренние каналы постоянного сечения, один – круг диаметром 3 см, второй – круг диаметром 10 см. В конце камер низкого давления устанавливались секции, являвшиеся естественным продолжением предыдущих, но снабженные смотровыми стеклами, датчиками давления и ионизационными датчиками.
Секции с каналом квадратного сечения использовались, прежде всего, для интерферометрических исследований. В этом случае в смотровой секции стекла устанавливались таким образом, что их внутренняя поверхность совпадала с плоскостью боковой стенки канала. В случае секций с круглым сечением стекла в смотровой секции устанавливались так, что их внутренняя поверхность являлась касательной к цилиндрической поверхности канала. В первом случае диаметр стекла составлял 1,6 см, толщина 1,5 см. Во втором случае чаще всего использовались окна из лейкосапфира или кварца диаметром 1,5 см и толщиной 1,5 – 2 мм (толщина кварца могла достигать 2 см). Диафрагмы изготавливались из твердой меди толщиной 1 – 3 мм. Для облегчения разрыва диафрагм на них делались либо фрезой, либо с помощью штампа 4 или 8 радиальных насечек глубиной от 0,2 до 1,5 мм (в зависимости от толщины диафрагмы и давления, при котором она должна разрываться). Принципиальная схема трактов вакуумирования и заполнения камер ударной трубы приведена на рис. 7.2.

Рис. 7.2.
Перед опытом камера низкого давления тщательно протиралась фланелью, смоченной с спирте-ректификате и откачивалась форвакуумным насосом до давления 10-2 мм рт.ст. Перед наполнением камера низкого давления несколько раз промывались исследуемым газом и затем наполнялась до нужного давления. Измерение начального давления осуществлялось с помощью образцового (В) и U – образного вакуумеров. Ошибка в измерении начального давления 7·10-2 мм рт.ст. Натекание из атмосферы составляло ~ 2·10-2 мм рт.ст./мин.
Камеры высокого давления и промежуточные, так же как и камеры низкого давления, перед опытом протирались спиртом, эфиром или ацетоном и откачивались форвакуумным насосом до давления 0,1 мм рт.ст. и заполнялись соответственно КВГС и гелием. Заполнение КВГС проводилось в таком порядке: сначала камеру заполняли кислородом, затем давали примерно половину гелия, затем – водород, после чего – остальную часть гелия. От момента заполнения до проведения опыта обычно проходило около 3 минут. Начальные давления в камерах высокого давления и промежуточной контролировались соответственно манометром (М) и мановакууметром (МВ). Инициирование воспламенения КВГС осуществлялось с помощью накаливания нихромовой проволоки (N) по которой во время опыта протекал ток от источника переменного напряжения (V), и нагревал ее.
Для выяснения наиболее эффективного режима работы двух диафрагменной ударной трубы и с целью получения максимальных скоростей ударных волн была проведена серия экспериментов, в которой варьировалось давление в промежуточной секции и прочность обеих диафрагм. Результаты этой серии экспериментов находятся в согласии с опубликованной уже после ее проведения работой [80]. Кроме того, была проведена серия экспериментов, в которой варьировалось соотношение водорода и гелия в КВГС, так что доля водорода изменялась от 20% до 90%, а гелия соответственно от 70% до нуля (общее давление в камере высокого давления оставлялось постоянными – 25 атм). Результаты этой серии экспериментов подтверждают мнение, высказанное в §1 о том, что замена в КВГС гелия водородом дает небольшой выигрыш в скорости.
Скорость ударной волны измерялась с помощью системы ионизационных датчиков. Ионизационный датчик состоит из двух электродов, изолированных друг относительно друга; один из электродов представляет собой металлический стержень диаметром около 1 мм, вторым является стенка ударной трубы. Расстояние между электродами 1÷2 мм. Электроды включены в цепь последовательно цепочке RC (R:104÷102ом; С:0, 005÷0,01 мкф), емкость которой перед опытом заряжается до напряжения 30÷100 в. При прохождении ударной волны электроды датчика замыкаются ионизированным газом, в цепи возникает разрядный ток, соответствующая разность потенциалов регистрируется осциллографом. На второй луч осциллографа подается синусоидальный сигнал известной частоты. По времени между соответствующими импульсами напряжения от двух ионизационных датчиков и расстоянию между ними определялась скорость ударной волны. Обычно использовалось четыре датчика. Первый ионизационный датчик запускал развертки, сигналы от трех других регистрировались одним из лучей осциллографа. Последний датчик, как правило, устанавливался в том сечении, где проводились основные измерения. Так, например, расстояния между последними тремя датчиками в случае однодиафрагменной ударной трубы (Ø 3 см) составляли соответственно 145 мм и 220 мм (последний датчик расположен на расстоянии 4 мм от торца). Синусоидальное напряжение известной частоты (0,25 – 1 мГц) подавалась от кварцевого генератора. Ошибка в измерении скорости не превышала ± 3%.
§4. Определение размеров ударно нагретой области и плотности среды за мощными ударными волнами.
Визуализация распространения разрывов – одна из самых существенных задач, возникающих при изучении мощных ударных волн. В этом отношении весьма перспективными представляются методы, в основу которых положена зависимость показателя преломления от параметров среды. Весьма чувствительным является метод Теплера, который позволяет хорошо визуализировать картину течения и измерять скорости перемещения скачков уплотнения. Однако определение параметров среды с помощью этого метода сопряжено с большими трудностями. Эти трудности обусловлены тем, что изменение интенсивности прошедшего света пропорционально производной показателя преломления. В случае оптически плотных плазм ослабление света может быть вызвано и непосредственно поглощением среды. Это поглощение в принципе может быть вычислено, если известны значения коэффициента поглощения среды, однако последнее условие далеко не всегда выполнено. Необходимо иметь в виду также, что на пленке непосредственно регистрируется ее почернение, связь которого с интенсивностью даже для монохроматического излучения весьма сложна. Использование немонохроматических источников света создает дополнительные трудности при вычислении плотности среды с помощью теплерограммы. Все эти обстоятельства, по-видимому, и явились причиной того, что в литературе отсутствуют сведения о непосредственном измерении параметров среды с помощью прибора Теплера. Исходя из изложенного, было отдано предпочтение интерферометрическому методу, где сдвиг полос на интерферограмме пропорционален изменению плотности среды. Этим фактом можно воспользоваться как для визуализации ударной волны и контактной области, так и для измерения распределения плотности за ударной волной.
Для этой цели была использована система Рождественского [81], в которой интерферометр Маха – Цендера скрещен со спектрографом. Применение спектрографа делает возможным наблюдение интерференции сразу на нескольких длинах волн, а это в сою очередь, позволяет не только определять расстояние между ударной волной и контактной областью, но и следить за ходом плотности. Эксперименты проводились с помощью ударной трубы с каналом квадратного сечения 26×26 мм.
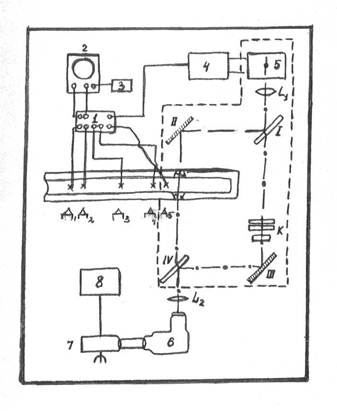
Рис. 7.3.
Схема эксперимента в случае использования интерферометра приведена на рис. 7.3. Излучение импульсного источника света (5) с помощью конденсора L1 формируется в плоско-параллельный поток, падает на первое полупрозрачное зеркало (1) и делится последним на два потока. Один из них отразившись от зеркала (II) проходит смотровую секцию ударной трубы. Второй отразившись от другого зеркала (III) проходит клиновой компенсатор К, который устанавливается для компенсации разности хода между этими потоками, вносимой смотровыми стеклами. После полупрозрачного зеркала (IV) оба потока объединяются и с помощью линзы L2 фокусируются на входную щель спектрографа (6). Вместо кассетной части спектрографа установлен ждущий фоторегистратор (7). Зеркала интерферометра укреплены в оправах, которые в свою очередь, установлены на специальных подставках. Юстировка зеркал осуществляется с помощью микрометрических винтов. Эта система установлена на швеллере шириной 40 см и длиной 250 см. Для исключения влияния посторонних вибраций интерферометр установлен на двух амортизаторах, аналогичных описанным в [84]. Амортизаторы стоят на винтах, которые позволяют устанавливать весь интерферометр горизонтально. Ждущий фоторегистратор (ЖФР) состоит из объектива (фокусное расстояние 50 или 75 см), двенадцатигранной призмы с зеркальными гранями и кассеты с фотопленкой, где регистрируется изображение. Призма вращалась со скоростью, которая составляла, в данных опытах, 375 об/с. Это позволяло регистрировать интерференционную картину с разрешающей способностью во времени около 0,3 мкс.
Импульсный источник света представляет собой разряд длиной линии в капилляре. Длинная линия состояла из 5-ти ячеек LC и заряжалась до 3 кВ. Капилляр изготовлен из текстолита толщиной 10 мм, диаметр его – 2 мм. Спектр излучения непрерывный с небольшим числом обращенных линий. При силе тока 10 кА распределение энергии в спектре источника совпадает (за исключением участков обращенных линий) с распределением энергии в спектре черного тела с температурой 39000К. Источник устанавливается в стандартном рейтере на стандартном рельсе.
Высота и ширина щели спектрографа составляет 150-200 мкм. Поскольку используются высокие порядки интерференции, то на фотопленке регистрируются почти вертикальные полосы. При пересечении одного из плеч интерферометра ударной волной или контактной областью происходит смещение интерференционной картины. Регистрация этих моментов времени на фотопленке позволяет определить расстояние между ударной волной и контактной областью.
Расстояние от диафрагмы до места регистрации составляло 220 см. Эта величина была выбрана исходя из того, что согласно [57] в случае турбулентного пограничного слоя длина ударно нагретой области здесь практически достигает своего максимального значения. В случае ламинарного слоя длина ударно нагретой области достигает максимального значения на расстояниях в 2-3 раза больших, однако удлинение камеры низкого давления в 2-3 раза нецелесообразно, вследствие того, что скорость ударной волны на таком расстоянии существенно уменьшается.
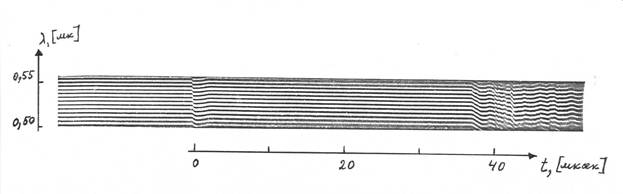
Рис. 7.4.
Интерферограмма, полученная при распространении ударной волны в аргоне (начальное давление 10 мм рт. ст.) со скоростью 4,3 км/с, приведена на рис. 7.4. Из рассмотрения интероферограммы видно, что сразу за резким сдвигом полос, связанным с передним фронтом ударной волны, следует зона изменения плотности, которая соответствует приходу среды к равновесию. Затем идет участок, где дальнейшего смещения интерференционных полос не наблюдается, т.е. плотность практически остается неизменной. За этим участком стабильных полос следует участок хаотических изменений интерференционной картины. Начало этого участка отождествлялось с приходом контактной области. За протяженность во времени ударно нагретой области принимался интервал между первым резким сдвигом интерференционной картины и началом хаотических колебаний интерференционных полос. Это время, умноженное на скорость ударной волны, дает величину ударно нагретой области. С увеличением скорости ударной волны зона релаксации уменьшается, полосы интерференционной картины начинают испытывать сначала небольшой, а затем и весьма значительный наклон, длина ударно нагретой области сокращается и при скоростях 7-8 км/с составляет 1,5-2 см. При таких высоких скоростях за передним фронтом ударной волны возникает сильное излучение, которое затрудняет изучение хода интерференционных полос в течении примерно одной мкс после их первого резкого сдвига.
Результаты измерений размеров ударно нагретой области в аргоне согласно [83] приведены на рис. 7.5. Здесь по оси ординат отложены размер ударно нагретой области в мм, по оси абсцисс скорость ударной волны в км/сек и соответствующие значения числа Маха. Темными кружками нанесены результаты, полученные при начальном давлении 1 мм рт. ст., светлыми – 10 мм рт. ст., наполовину темными – 50 мм рт. ст. Пунктирной кривой даны значения равные половине длины ударно нагретой области в идеальном случае. Эта кривая позволяет провести сравнение реальных значений этой области с размерами в идеальном случае, а также с результатами [84], где получено, что реальные значения ударно нагретой области за счет перемешивания на границе с контактной областью примерно вдвое меньше размеров в идеальном случае. Напомним, что это соотношение было установлено для небольших скоростей и как видно из сопоставления пунктирной кривой и экспериментальных данных для начальных давлений 10 и 50 мм рт. ст. результаты [84] и эти данные в области чисел Маха 10-12 согласуются между собой. Для начального давления 1 мм рт. ст. во всем исследованном диапазоне чисел Маха, а также для 10 и 50 мм рт. ст. при числах Маха выше 15, реальные значения длины ударно нагретой области существенно меньше, чем это следует из [84], причем для скоростей около 7-8 км/сек экспериментальные данные лежат примерно в пять-шесть раз ниже пунктирной кривой. Аналогичные результаты получены для воздуха [85].

Рис. 7.5.
Исследования плотности проводились как за падающими, так и за отраженными ударными волнами, однако предпочтение было отдано исследованиям за отраженными ударными волнами, поскольку, как отмечено в § 2, в этом случае участок формирования практически отсутствует. Влияние области бифуркации можно свести к минимуму, если проводить исследования достаточно близко от торца. Кроме того, отметим, что среду за отраженной ударной волной можно считать покоящейся в лабораторной системе координат, а следовательно относить полученные результаты непосредственно к состоянию за фронтом ударной волны.
Интерферограммы, полученные по методике, изложенной выше, позволяют определить плотность плазмы за ударными волнами. С этой целью в спектре были выбраны длины волн: 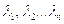 , отвечающие максимумам освещенности до прихода ударной волны. Число n определяется числом компонент среды, концентрации которых нужно определить. Для этих длин волн справедливы соотношения:
, отвечающие максимумам освещенности до прихода ударной волны. Число n определяется числом компонент среды, концентрации которых нужно определить. Для этих длин волн справедливы соотношения:
а) до прихода ударной волны –
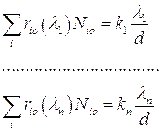 (7.3)
(7.3)
б) после прихода ударной волны –
 (7.4)
(7.4)
здесь:
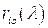 ,
, 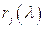 ,
,  – соответственно рефракции нейтральных, ионных и электронных компонент в пересчете на одну нейтральную частицу, ион или электрон,
– соответственно рефракции нейтральных, ионных и электронных компонент в пересчете на одну нейтральную частицу, ион или электрон,
 - концентрации нейтральных частиц соответственно до и после прихода ударной волны,
- концентрации нейтральных частиц соответственно до и после прихода ударной волны,
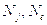 - концентрации ионов и электронов соответственно,
- концентрации ионов и электронов соответственно,
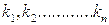 – порядки интерференции, взятые с учетом сдвига, обусловленного неидентичностью плеч интерферометра,
– порядки интерференции, взятые с учетом сдвига, обусловленного неидентичностью плеч интерферометра,
 - изменения порядка интерференции, связанные с приходом ударной волны,
- изменения порядка интерференции, связанные с приходом ударной волны,
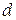 – расстояние между окнами смотровой секции.
– расстояние между окнами смотровой секции.
При написании системы уравнений (7.4), положено, что вклад в рефракцию возбужденных частиц не сильно отличается (в пересчете на одну частицу) от вклада соответствующих частиц в невозбужденном состоянии.
Вычитая почленно из первого уравнения системы (7.3) первое уравнение системы (7.4), из второго уравнения системы (7.3) второе уравнение системы (7.4) и т.д., получим:
 (7.5)
(7.5)
Эта система уравнений позволяет найти  , если известны
, если известны 
В случае воздуха формулу, определяющую рефракцию целесообразно записать, используя плотность, положив
 (7.6)
(7.6)
где  – рефракции отдельных компонент воздуха в расчете на одну частицу.
– рефракции отдельных компонент воздуха в расчете на одну частицу.
Постоянную Гладстона – Дейла «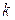 » можно считать неизменной только тогда, когда при изменении параметров среды не происходит возбуждения внутренних степеней свободы, химических реакций, диссоциации или ионизации. В противном случае необходим дополнительный анализ. За падающей ударной волной в воздухе вплоть до чисел Маха 25 концентрация свободных электронов согласно [86,87] не должна превышать 0,2%, поэтому влиянием электронов на рефракцию в этих условиях можно пренебречь. Согласно [87] значение «
» можно считать неизменной только тогда, когда при изменении параметров среды не происходит возбуждения внутренних степеней свободы, химических реакций, диссоциации или ионизации. В противном случае необходим дополнительный анализ. За падающей ударной волной в воздухе вплоть до чисел Маха 25 концентрация свободных электронов согласно [86,87] не должна превышать 0,2%, поэтому влиянием электронов на рефракцию в этих условиях можно пренебречь. Согласно [87] значение «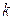 » для атомарного кислорода на 6% меньше по сравнению с молекулярным кислородом, тогда как для атомарного азота «
» для атомарного кислорода на 6% меньше по сравнению с молекулярным кислородом, тогда как для атомарного азота «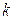 » на 28% больше, чем для молекулярного. Учитывая, что влияние диссоциации азота и кислорода на рефракцию частично компенсируется, а также, что молекулы азота составляют только четыре пятых от общего числа частиц в воздухе, можно ожидать, что изменение значения постоянной Гладстона – Дейла в случае воздуха, нагретого падающими ударными волнами вплоть до чисел Маха 25, будет мало. Этот вывод был подтвержден непосредственными расчетами, результаты которых приведены в таблице 7.1. Значения температуры, давления, плотности и концентраций компонент воздуха за падающими ударными волнами были взяты из таблиц [89-93] удельные рефракции компонент воздуха – согласно [86,87].
» на 28% больше, чем для молекулярного. Учитывая, что влияние диссоциации азота и кислорода на рефракцию частично компенсируется, а также, что молекулы азота составляют только четыре пятых от общего числа частиц в воздухе, можно ожидать, что изменение значения постоянной Гладстона – Дейла в случае воздуха, нагретого падающими ударными волнами вплоть до чисел Маха 25, будет мало. Этот вывод был подтвержден непосредственными расчетами, результаты которых приведены в таблице 7.1. Значения температуры, давления, плотности и концентраций компонент воздуха за падающими ударными волнами были взяты из таблиц [89-93] удельные рефракции компонент воздуха – согласно [86,87].
Таблица 7.1.
М |
10 |
15 |
20 |
25 |
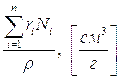
|
0,226 |
0,228 |
0,237 |
0,246 |
При нормальных условиях константа Гладстона – Дейла k=0,227 см3/г.
Таким образом, воспользовавшись соотношением (7.6) можно написать систему уравнений аналогичную (7.5):
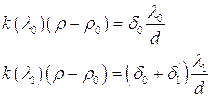 (7.7)
(7.7)
где 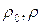 – соответственно плотности перед и за ударной волной.
– соответственно плотности перед и за ударной волной.
Отсюда следует:
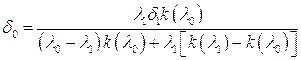 (7.8)
(7.8)
Отметим, что согласно [87], рефракции атомарных азота и кислорода не зависят от длины волны, а для молекулярного азота и кислорода справедлива формула Коши:
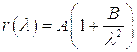 (7.9)
(7.9)
причем: 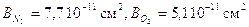 . Воспользовавшись этим, можно показать, что
. Воспользовавшись этим, можно показать, что
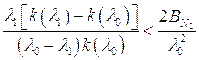 (7.10)
(7.10)
для  ,
,  , т.е. вместо (7.8) можно принять:
, т.е. вместо (7.8) можно принять:
 (7.11)
(7.11)
Округлив полученное значение 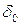 до целого числа, с помощью первого из уравнений (7.7) можно найти плотность воздуха и за ударной волной.
до целого числа, с помощью первого из уравнений (7.7) можно найти плотность воздуха и за ударной волной.
Как следует из (7.7) ошибка измерения плотности в этом случае равна:
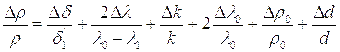 (7.12)
(7.12)
При абсолютной ошибке измерения сдвига 0,05  может составлять 1%÷5%; положив
может составлять 1%÷5%; положив 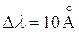 , найдем, что величина второго слагаемого может составлять 1%-5%;
, найдем, что величина второго слагаемого может составлять 1%-5%;  не превышает, как это следует из таблицы 2 – 9%; сумма последних трех слагаемых не превышает 1,5%. Необходимо иметь в виду, что при небольших значениях числа Маха,
не превышает, как это следует из таблицы 2 – 9%; сумма последних трех слагаемых не превышает 1,5%. Необходимо иметь в виду, что при небольших значениях числа Маха,  невелико и поэтому сумма первых двух слагаемых может достигать 10%, однако
невелико и поэтому сумма первых двух слагаемых может достигать 10%, однако  в этом случае не превышает 1% - 2%. При числах Маха 20-25 сумма первых двух слагаемых уменьшается до 2%, однако отклонение константы Гладстона – Дейла от значения, принятого в расчетах, как это следует из табл. 7.1. может достигнуть 9% и носит систематический характер.
в этом случае не превышает 1% - 2%. При числах Маха 20-25 сумма первых двух слагаемых уменьшается до 2%, однако отклонение константы Гладстона – Дейла от значения, принятого в расчетах, как это следует из табл. 7.1. может достигнуть 9% и носит систематический характер.
Таким образом, ошибка при определении плотности воздуха с помощью системы уравнений (7.7) остается в диапазоне чисел Маха 10-25 примерно постоянной и не превышает 12 %, однако в области чисел Маха 20-25 следует ожидать небольшого систематического превышения экспериментальных данных над расчетными.
Результаты измерений плотности в воздухе непосредственно за ударной волной приведены на рис. 7.6. (начальное давление 5 мм рт.ст). Кривая расчетные значения согласно [92,93]. Как видно из сопоставления экспериментальных и расчетных данных, они находятся в согласии. Систематическое превышение экспериментальных данных над расчетными при числах М>20 объясняется, по-видимому, как это отмечалось выше, отклонением константы Гладстона – Дейла от значения, принятого при обработке экспериментальных данных.

Рис. 7.6.
Полученные на основе экспериментальных данных распределения плотности вдоль ударно нагретой области приведены на рис. 7.7. начальное давление 5 мм рт.ст. здесь обозначено: 0 – М = 10.2, · – М = 16.6, 0 – М = 21.4.
По оси абсцисс отложено отношение расстояния от ударной волны к длине всей ударно нагретой области. Эта длина была взята в соответствии с экспериментальными данными, полученными по методике, описанной выше. Из рассмотрения рис. 7.7. следует, что плотность воздуха остается постоянной практически во всей ударно нагретой области. Таким образом, предсказанное в [59] увеличение плотности в первой трети ударно нагретой области не обнаружено. Некоторое увеличение в начале ударно нагретой области имеет место только при небольших скоростях и связано по-видимому с релаксационными явлениями за передним фронтом ударной волны.

Рис. 7.7.
Определение плотности воздуха за отражением ударными волнами при числах M≤16 проводилось с помощью соотношений (7.7). При более высоких скоростях ударных волн становится существенным вклад в рефракцию, обусловленный появлением свободных электронов. Поскольку масса электронов пренебрежимо мала, то можно записать следующую систему уравнений:
 (7.13)
(7.13)
отсюда следует:
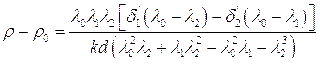 (7.14)
(7.14)
Точность определения плотности с помощью системы уравнений (7.13), оцененная аналогично предыдущему, составляет 24%.
Определенные по этой методике значения плотности и электронных концентраций при М<16 приведены соответственно на рис. 7.8. – 7.9. (начальное давление 5 мм рт.ст.).
На рис. 7.10. приведен временной ход плотности за отраженными ударными волнами в воздухе при начальном давлении 5 мм рт.ст.. Обозначения: · – М = 10; 0 – М = 15,5; 0 – М = 21,4. По оси ординат отложено отношение плотности в данный момент времени, к плотности, имевшей место непосредственно за отраженной ударной волной. Как видно из рис. 7.10. плотность остается практически постоянной в течении всего промежутка времени пока удается наблюдать интерференционные полосы. Аналогичные результаты в случае аргона получены в [88].

Рис. 7.8
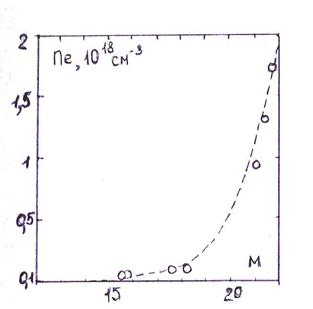
Рис. 7.9
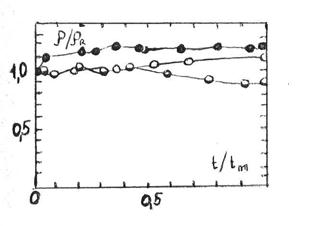
Рис. 7.10
§5. Измерение температуры за мощными ударными волнами.
В основу метода положен закон Кирхгофа:
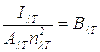 (7.15)
(7.15)
где  - монохроматическая излучательная способность объекта,
- монохроматическая излучательная способность объекта,
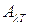 - его монохроматическая поглощательная способность,
- его монохроматическая поглощательная способность,
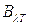 - монохроматическая излучательная способность черного тела, функция Планка
- монохроматическая излучательная способность черного тела, функция Планка
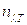 - показатель преломления среды; для рассматриваемых ниже
- показатель преломления среды; для рассматриваемых ниже
плазм 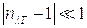 , поэтому
, поэтому  в (7.15) можно опустить.
в (7.15) можно опустить.
Существо метода состоит в том, что одновременно измеряются монохроматические излучательная и поглощательная способности, что позволяет вычислить для каждого момента времени значения функции Планка, а, следовательно, и температуру объекта. Поскольку для измерения температуры с помощью закона Кирхгофа необходимо измерять излучательную и поглощательную способность для одной и той же фиксированной длины волны, то элементы оптической системы (линзы, светофильтры, монохроматоры) были общими при измерении как излучательной, так и поглощательной способности. Схема экспериментальной установки для измерения температуры дана на рис. 7.11.
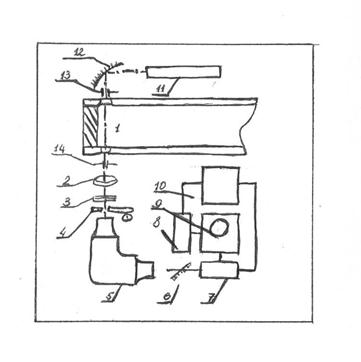
Рис. 7.11
Для измерения излучательной способности центр излучающего объема (1) проецируется линзой (2) на входную щель монохроматора (5). Затем излучение преобразуется фотоумножителем (7) в электрический сигнал и регистрируется одним из лучей двухлучевого осциллографа (9). Этот канал градуируется перед каждым опытом в абсолютных единицах с помощью ленточной вольфрамовой лампы и стробоскопа (4). Ленточная вольфрамовая лампа устанавливается в те же оптические условия, что и исследуемый объект. Нейтральные светофильтры (3) позволяют в широких пределах изменять чувствительность регистрирующей системы. Для измерения поглощательной способности используется гелий-неоновый оптический квантовый генератор (ОКГ) (II). Луч ОКГ, отразившись от собирающего зеркала (12), проходит исследуемый газ, в котором частично поглощается. Это изменение интенсивности регистрируется системой, состоящей из линзы (2), нейтральных светофильтров (4), монохроматора (5), поворотной призмы и фотоумножителя (8). Получающийся в результате импульс напряжения записывается вторым лучом осциллографа (9). Питание фотоумножителей осуществляется высоковольтным стабилизированным выпрямителем (10). Диафрагмы (13) и (14) позволяют улучшить пространственное разрешение.
Для независимого измерения излучательной и поглощательной способности исследуемого газа входная и выходная щели монохроматора по высоте разделены на две части, высоты которых 1 мм и 3 мм. Для измерения излучательной способности использовался участок вблизи λ=6328Å с полушириной 5Å; полуширина линии, излучаемой ОКГ, порядка 0.1Å.. Отсюда следует, что излучательная и поглощательная способность измерялась на участках спектра различной ширины и применение закона Кирхгофа в этом случае может быть оправдано только в том случае, если эти величины на указанных выше участках спектра изменяются не сильно, так что их средние значения на участках 0.1Å и 5Å отличаются несущественно. Поэтому применению данного метода должен предшествовать анализ спектрального состава излучения плазмы, температуру которой предполагается измерить. Кроме того, необходим анализ состояния объекта, который должен дать ответ на вопрос о том находится ли объект в состоянии локального термодинамического равновесия.
Оптическая система имеет конечную апертуру, что обуславливает конечное время нарастания сигналов. Это время составляет в случае отраженных ударных волн для канала излучения 5-7 мксек, для канала поглощения 3-5 мксек. Время нарастания сигнала для канала излучения обусловлено заполнением апертуры оптической системы, для канала поглощения-временем, за которое отраженная волна проходит диаметр луча ОКГ. Очевидно, что в общем случае эти интервалы времени различны. Ясно также, что соответствующие участки осциллограмм должны быть исключены из рассмотрении.
После пересечения ударной волной границ луча ОКГ и заполнения апертуры оптической системы канал поглощения регистрирует величину:
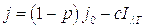 (7.16)
(7.16)
где  - пропускание изучаемого объекта,
- пропускание изучаемого объекта,
 - излучательная способность ОКГ,
- излучательная способность ОКГ,
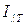 - излучательная способность плазмы
- излучательная способность плазмы
 - отношение чувствительностей каналов поглощения и излучения (обычно значения «
- отношение чувствительностей каналов поглощения и излучения (обычно значения « » лежат в интервале 0,05
» лежат в интервале 0,05 0,1).
0,1).
Отметим, что в случае 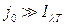 и
и 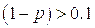 второй член играет роль поправки. В противном случае этот член должен быть определен достаточно точно. Излучательная способность плазмы измеряется в том же опыте по каналу излучения. Величина «
второй член играет роль поправки. В противном случае этот член должен быть определен достаточно точно. Излучательная способность плазмы измеряется в том же опыте по каналу излучения. Величина «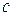 » должна быть определена путем дополнительных опытов, в которых один и тот же световой поток от эталонной лампы, либо исследуемого объекта, направляется одновременно и в канал поглощения и в канал излучения. После этого с помощью (7.16) может быть определена величина
» должна быть определена путем дополнительных опытов, в которых один и тот же световой поток от эталонной лампы, либо исследуемого объекта, направляется одновременно и в канал поглощения и в канал излучения. После этого с помощью (7.16) может быть определена величина  , которую обозначим
, которую обозначим  . Эта величина в общем случае складывается из нескольких величин:
. Эта величина в общем случае складывается из нескольких величин:
 (7.17)
(7.17)
где  - поглощательная способность плазмы,
- поглощательная способность плазмы,
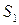 - изменение сигнала, вызванное изменением показателя преломления на фронте ударной волны,
- изменение сигнала, вызванное изменением показателя преломления на фронте ударной волны,
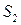 - изменение сигнала, обусловленное рассеянием среды,
- изменение сигнала, обусловленное рассеянием среды,
 - коэффициент отражения исследуемого объекта.
- коэффициент отражения исследуемого объекта.
Величина  может быть оценена исходя из данных, получаемых с помощью прибора Теплера. Такая оценка показывает, что в наших экспериментах луч ОКГ отклоняется на величину, не превышающую 0,1 мм. Это не могло привести к изменению сигнала более, чем на 1%. Кроме того, были поставлены контрольные опыты, в которых луч ОКГ направлялся таким образом, что его граница касалась границы входной щели либо слева, либо справа. Если бы смещение луча во время опыта существенно превышало 0,1 мм, то в контрольных опытах на экране осциллографа регистрировалось бы увеличение интенсивности. Это увеличение интенсивности зарегистрировано не было, следовательно,
может быть оценена исходя из данных, получаемых с помощью прибора Теплера. Такая оценка показывает, что в наших экспериментах луч ОКГ отклоняется на величину, не превышающую 0,1 мм. Это не могло привести к изменению сигнала более, чем на 1%. Кроме того, были поставлены контрольные опыты, в которых луч ОКГ направлялся таким образом, что его граница касалась границы входной щели либо слева, либо справа. Если бы смещение луча во время опыта существенно превышало 0,1 мм, то в контрольных опытах на экране осциллографа регистрировалось бы увеличение интенсивности. Это увеличение интенсивности зарегистрировано не было, следовательно,  . Величина
. Величина 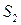 также не превышает 0,01. В пользу того, что рассеяние плазмы мало, свидетельствует тот факт, что увеличение длины электрической дуги при прочих равных условиях не ведет к росту интенсивности излучения при регистрации излучения вдоль радиуса дуги [94]. В наших экспериментах также не наблюдалось возрастания интенсивности с ростом объема газа, нагретого отраженной ударной волной, следовательно, если рассеяние и имеет место, то оно настолько мало, что увеличение интенсивности, обусловленное рассеянием, много меньше уменьшения интенсивности, обусловленного уменьшением температуры.
также не превышает 0,01. В пользу того, что рассеяние плазмы мало, свидетельствует тот факт, что увеличение длины электрической дуги при прочих равных условиях не ведет к росту интенсивности излучения при регистрации излучения вдоль радиуса дуги [94]. В наших экспериментах также не наблюдалось возрастания интенсивности с ростом объема газа, нагретого отраженной ударной волной, следовательно, если рассеяние и имеет место, то оно настолько мало, что увеличение интенсивности, обусловленное рассеянием, много меньше уменьшения интенсивности, обусловленного уменьшением температуры.
Оценка коэффициента отражения, проведенная с помощью формул Френеля, показывает, что  .
.
Таким образом, в данном случае сумма второго, третьего и четвертого слагаемых не превышает 0,01-0,02, т.е. этими слагаемыми можно пренебречь и положить 
Источником систематических ошибок может служить также неоднородность исследуемого объекта вдоль оптической оси системы. Около внутренней стенки ударной трубы после отражения ударной волны от торца образуется область, где температура резко падает от максимальной (на внутренней границе области) до температуры стенки ударной трубы. В экспериментах ось оптической системы проходила от торца ударной трубы не далее, чем 5 мм, где ширина промежуточной области не превышает 1 мм [95]. Отметим, что коэффициенты поглощения плазмы в непрерывном спектре пропорциональны квадрату концентрации электронов, которая в свою очередь экспоненциально зависит от температуры. Поэтому роль пристенной области сводится к уменьшению размеров плазмы вдоль оптической оси на величину, не превышающую 2%, т.е. ошибкой, обусловленной наличием этой области можно пренебречь. Случайная ошибка измерения температуры определяется соотношением:
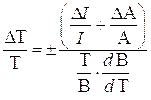 (7.18)
(7.18)
где 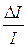 - относительная ошибка измерения излучательной способности,
- относительная ошибка измерения излучательной способности,
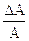 - относительная ошибка измерения поглощательной способности,
- относительная ошибка измерения поглощательной способности,
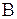 - функция Планка.
- функция Планка.
Ошибка измерения излучательной способности определяется ошибкой измерения импульсных напряжений с помощью осциллографа и возможной неточностью установки эталонного источника. Первая, согласно гарантии завода-изготовителя, не должна превышать 10%. Непосредственные измерения, проведенные путем многократного измерения импульсов напряжения, подаваемых на осциллограф от генератора стандартных сигналов, дали, для использованного в настоящих экспериментах экземпляра осциллографа, величину ошибки 3%. Погрешность при тарировке, обусловленная неточностью установки эталонного источника света, составляет примерно 3%. Ошибка измерения поглощательной способности определяется также ошибкой измерения импульсных напряжений с помощью осциллографа, но для небольших значений  (~0,15) эта ошибка может достигать 10-12%, тогда как для больших значений
(~0,15) эта ошибка может достигать 10-12%, тогда как для больших значений 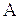 она будет составлять тоже 3%. Поэтому в целом величина, стоящая в числителе формулы (7.18) при T=12000К, составляет 20-21%, при Т=20000К - 13-14%. Знаменатель в формуле (7.18) наоборот уменьшается с ростом температуры, так что ошибка в измерении остается примерно постоянной в диапазоне 12000-20000К и составляет 7-8%.
она будет составлять тоже 3%. Поэтому в целом величина, стоящая в числителе формулы (7.18) при T=12000К, составляет 20-21%, при Т=20000К - 13-14%. Знаменатель в формуле (7.18) наоборот уменьшается с ростом температуры, так что ошибка в измерении остается примерно постоянной в диапазоне 12000-20000К и составляет 7-8%.
Рассмотрим результаты измерения температуры за отраженными ударными волнами в аргоне. Необходимой предпосылкой изложенного выше метода измерения температуры является достаточно плавное изменение излучательной и поглощательной способности на тех участках спектра, где производится измерение этих величин. Анализ спектрограмм, полученных в этих условиях, показал, что в области около 6328Å отсутствуют линии и полосы атомарных и молекулярных примесей и это делает применение закона Кирхгофа к измеренным в данном случае значениям излучательной и поглощательной способности оправданным.
Закон Кирхгофа предполагает, что имеет место равновесное распределение энергии по степеням свободы. Времена релаксации ионизации, которые для установления равновесия в аргоне при температурах 10000-20000К и давлениях в несколько десятков атмосфер, имеют решающее значение, в данном случае не превышает 1 мкс, поэтому первые 1-2 мкс на осциллограммах должны быть исключены из рассмотрения.

Рис. 7.12.
На рис.7.12 приведены осциллограммы излучательной и поглощательной способности аргона, нагретого отраженной ударной волной в ударной трубе диаметром 100 мм при числе Маха падающей ударной волны, равном 14 и начальном давлении 10 мм рт.ст. Как следует из рассмотрения рис.7.12, излучательная способность, достигнув максимума, остается в течение ~30 мкс постоянной, затем в течение ~60 мкс она медленно уменьшается; поглощательная способность, достигнув максимума, остается практически постоянной (~100 мкс), т.е. изменение значений температуры на этом отрезке времени будет определяться, прежде всего, изменением интенсивности. Примерно через 100 мкс поглощательная способность снова начинает возрастать. Это явление, отмечавшееся и ранее в [96] и названное «вторичным» поглощением, по времени примерно совпадает с моментом прихода в данное сечение ударной трубы возмущений, обусловленных встречей отраженной ударной волны с контактной областью. При более высоких числах Маха вид осциллограммы остается аналогичным. Отличие заключается в том, что излучательная способность уменьшается быстрее, а «вторичное» поглощение начинается раньше, т.к. отраженная ударная волна раньше встречается с контактной областью.
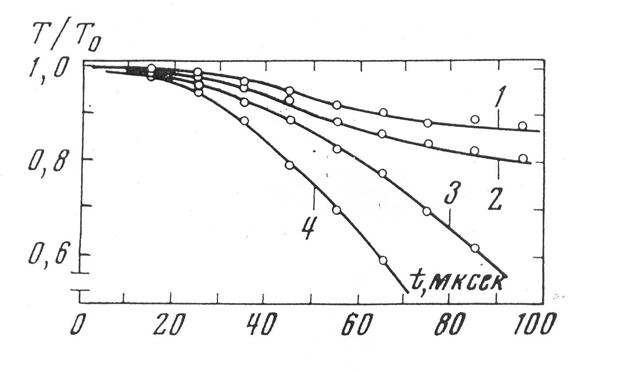
Рис. 7.13.
Полученные осциллограммы были обработаны с учетом изложенного выше. На рис. 7.13 приведены полученные в результате обработки зависимости от времени температуры аргона в области, отстоящей от торца ударной трубы на 5 мм при начальном давлении 10 мм рт. ст. Здесь дано отношение значения температуры в данный момент к начальному значению температуры. В качестве начала отсчета времени выбран тот момент, когда можно было считать, что отраженная ударная волна не только пересекла границы луча ОКГ, но и границы телесного угла, из которого поступает излучение в канал измерения излучательной способности. Следует отметить, что ошибка при измерении относительных значений температуры примерно вдвое меньше, чем ошибка измерения абсолютных значений, поскольку в этом случае исключаются ошибки, связанные с проведением абсолютных измерений. Таким образом, точность, с которой получены приведенные на рис. 7.13 кривые, не хуже 4%. Как следует из рассмотрения этих кривых при небольших числах Маха (М<II) температура аргона за отраженной ударной волной остается в течение ~50 мкс в пределах ошибок измерения постоянной (кривая 1). С ростом числа Маха падающей ударной волны это время уменьшается и при М=16,5 составляет около 20 мкс. Полученные данные не противоречат результатам работы [63,64], однако, строгое сопоставление затруднительно, т.к. в [63,64] рассчитаны профили температуры аргона за падающей ударной волной. Следует подчеркнуть, что в настоящих экспериментах не обнаружено немонотонного изменения температуры за отраженной ударной волной, отмечавшегося в [97]. Этот немонотонный ход значений, температуры во времени, по-видимому, связан с неоднородным распределением по пространству элемента (Na,Ba), по линии которого велись пирометрические исследования.
На рис. 7.14 приведены экспериментальные значения температуры аргона (точки), измеренные с помощью закона Кирхгофа и относящиеся к тем участкам, где, согласно рис.7.13, температуру можно считать постоянной. Как видно, из сопоставления этих значений с результатами расчетов [98] имеет место согласие между экспериментальными и расчетными данными.
Аналогичные изменения температуры были проведены при распространении ударных волн в воздухе и двуокиси углевода; результаты этих экспериментов приведены в [99].
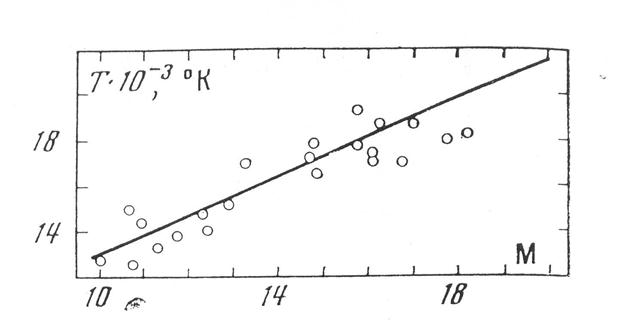
Рис. 7.14
§6. Измерение давления за ударными волнами.
В основу метода измерения давления был положен пьезоэлектрический эффект. Разность потенциалов, возникшая на обкладках пьезоэлемента в результате действия внешней силы, обусловлена его поляризацией, а последняя - механическим напряжением, вызванным внешней силой. В общем случае механическое напряжение в кристалле описывается тензором второго ранга 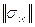 , а возбужденная им поляризация вектором
, а возбужденная им поляризация вектором  . Компоненты этого вектора -
. Компоненты этого вектора -  связаны с компонентами
связаны с компонентами  линейными соотношениями вида [100]:
линейными соотношениями вида [100]:
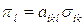 (7.19)
(7.19)
причем  является тензором третьего ранга, компоненты которого именуют пьезоэлектрическими модулями. Для пьезокварца, керамик из титаната и цирконата бария в случае однородной линейной деформации (например, вдоль оси цилиндра -
является тензором третьего ранга, компоненты которого именуют пьезоэлектрическими модулями. Для пьезокварца, керамик из титаната и цирконата бария в случае однородной линейной деформации (например, вдоль оси цилиндра -  ), соотношение (7.19) приобретает простой вид:
), соотношение (7.19) приобретает простой вид:
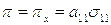 (7.20)
(7.20)
Связь между механическим напряжением и внешней силой в общем случае для тела произвольной формы, находящегося под воздействием внешней силы, произвольно зависящей от координат и времени, исключительно сложна. Эта связь задается законом Гука и уравнением в частных производных второго порядка для компонент вектора смещения с граничными условиями, записанными в самом общем виде. Наиболее простой вид эта связь приобретает в случае однородного стержня длиною  , к концу которого вдоль оси приложена переменная сила
, к концу которого вдоль оси приложена переменная сила  . Решение этой задачи согласно [102] для моментов времени, лежащих в интервале
. Решение этой задачи согласно [102] для моментов времени, лежащих в интервале  , имеет вид:
, имеет вид:
для 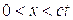 :
:
 (7.21)
(7.21)
для 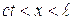
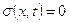
где 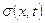 - напряжение вдоль стержня в точке с координатой
- напряжение вдоль стержня в точке с координатой 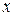 ,
,
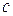 - скорость распространения упругих деформаций,
- скорость распространения упругих деформаций,
 - константа.
- константа.
Соотношения (7.21) констатируют тот факт, что по стержню распространяется волна механических напряжений, форма которой полностью соответствует зависимости приложенной к его торцевой поверхности силы от времени. Величина напряжения на расстоянии 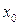 от начала стержня в момент
от начала стержня в момент 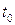 прямо пропорциональна тому значению, силы, которое она имела в момент
прямо пропорциональна тому значению, силы, которое она имела в момент  . Эта ситуация будет иметь место до тех пор пока фронт волны, отразившись от свободного конца стержня не возвратится в точку
. Эта ситуация будет иметь место до тех пор пока фронт волны, отразившись от свободного конца стержня не возвратится в точку 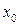 . Если в точке
. Если в точке 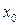 установлен пьезоэлемент, акустической импеданс которого равен акустическому импедансу стержня, причем так, что пьезокерамика плотно соприкасается с материалом стержня, то волна механических напряжений будет распространяться не испытывая искажений.
установлен пьезоэлемент, акустической импеданс которого равен акустическому импедансу стержня, причем так, что пьезокерамика плотно соприкасается с материалом стержня, то волна механических напряжений будет распространяться не испытывая искажений.
Учитывая, что разность потенциалов на обкладках пьезоэлемента - 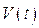 прямо пропорциональна заряду, который в свою очередь- поляризации пьезоэлемента, а также принимая во внимание соотношения (7.20-7.21), для
прямо пропорциональна заряду, который в свою очередь- поляризации пьезоэлемента, а также принимая во внимание соотношения (7.20-7.21), для 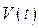 можно написать:
можно написать:
для 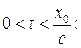
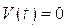 (7.22)
(7.22)
для 

для  :
:

где 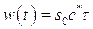 - часть объема пьезоэлемента, заключенная между передней границей пьезоэлемента и фронтом волны напряжений,
- часть объема пьезоэлемента, заключенная между передней границей пьезоэлемента и фронтом волны напряжений,
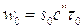 - объем всего пьезоэлемента,
- объем всего пьезоэлемента,
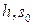 - соответственно высота пьезоэлемента и площадь его поперечного сечения, равная площади поперечного сечения стержня,
- соответственно высота пьезоэлемента и площадь его поперечного сечения, равная площади поперечного сечения стержня,
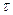 - интервал времени между моментом пересечения волной передней границы пьезоэлемента и моментом t,
- интервал времени между моментом пересечения волной передней границы пьезоэлемента и моментом t,
 - время распространения волны по пьезоэлементу,
- время распространения волны по пьезоэлементу,
 - константа.
- константа.
Ограничимся рассмотрением только таких функций 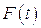 , изменением которых в течение интервала времени
, изменением которых в течение интервала времени  можно пренебречь, также такими воздействиями, что можно положить
можно пренебречь, также такими воздействиями, что можно положить 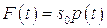 , где
, где 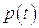 - давление на торец стержня.
Тогда соотношения (7.22) преобразуются к виду:
- давление на торец стержня.
Тогда соотношения (7.22) преобразуются к виду:
для 
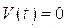 (7.23)
(7.23)
для 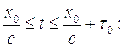
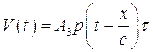
для 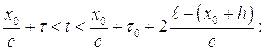
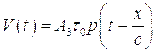
где  - константа.
- константа.
Таким образом, разность потенциалов на обкладках пьезоэлемента, установленного в точке 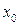 стержня с импедансом равным импедансу пьезоэлемента, будет следовать до момента
стержня с импедансом равным импедансу пьезоэлемента, будет следовать до момента 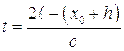 за ходом давления Р(t) с запаздыванием
за ходом давления Р(t) с запаздыванием  , если изменением
, если изменением 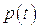 за время
за время 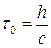 можно пренебречь.
можно пренебречь.
Обратимся теперь к ударным волнам. В этом случае возможны два варианта:
- Ударная волна падает нормально на торец ударной трубы и затем отражается. Стержень с пьезоэлементами установлен так, что его торцевая поверхность совпадает с поверхностью торца. Время, в течение которого давление изменяется от начального значения за отраженной волной не превышает 1 мкс. В этом случае для пьезоэлементов с
 мм нельзя гарантировать, что участок первоначального нарастания
мм нельзя гарантировать, что участок первоначального нарастания  будет связано с
будет связано с 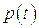 последним из соотношений (7.23) вплоть до
последним из соотношений (7.23) вплоть до  .
.
- Ударная волна проходит мимо торца стержня, установленного в стенке ударной трубы.
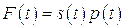 , где
, где 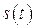 - площадь той части торцевой поверхности датчика, на которую воздействует среда за ударной волной. Для скоростей ударных волн, порядка нескольких км/с и диаметра стержня, порядка нескольких мм, время, в течение которого
- площадь той части торцевой поверхности датчика, на которую воздействует среда за ударной волной. Для скоростей ударных волн, порядка нескольких км/с и диаметра стержня, порядка нескольких мм, время, в течение которого  изменяется за счет прохождения ударной волны мимо датчика (даже если давление за волной остается постоянным), будет составлять величину порядка 1 мкс, т.е. для
изменяется за счет прохождения ударной волны мимо датчика (даже если давление за волной остается постоянным), будет составлять величину порядка 1 мкс, т.е. для  мм сравнимую с
мм сравнимую с  . Следовательно, и в этом варианте, также как и в предыдущем нельзя гарантировать, что, участок первоначального нарастания
. Следовательно, и в этом варианте, также как и в предыдущем нельзя гарантировать, что, участок первоначального нарастания  будет отражать ход давления за ударной волной. Однако далее вплоть до момента
будет отражать ход давления за ударной волной. Однако далее вплоть до момента 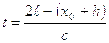 последнее из соотношений (7.26) будет справедливо.
последнее из соотношений (7.26) будет справедливо.
Таким образом, с помощью датчика, построенного на изложенных выше принципах, можно измерять давление, но только после того как закончилось первоначальное нарастание сигнала. Постоянная времени такого датчика будет равна  , разрешение по пространству-
, разрешение по пространству-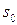 , запаздывание электрического сигнала по отношению к исходному воздействию -
, запаздывание электрического сигнала по отношению к исходному воздействию - 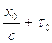 . Эти принципы были положены в основу конструкции датчика.
. Эти принципы были положены в основу конструкции датчика.
В качестве чувствительного элемента датчика давления использовался пьезоэлемент, изготовленный из цирконата- титаната свинца марки ЦТС-19 в виде цилиндрического столбика диаметром 5 мм и высотой 2 мм. Плоские поверхности пьезоэлемента покрыты серебром. Пьезоэлемент устанавливался между двумя стержнями из латуни марки Л-59. Длина первого - 15 мм, второго - 500 мм, диаметр стержней - 5 мм. Импеданс латуни равен 3,04·1011 г/(см2·c) , импеданс керамики ЦТС-19 близок этому значению. Для обеспечения надежного акустического контакта торцевые поверхности латунных стержней, обращенные к пьезоэлементу, тщательно притирались с помощью специальной пасты. Высокая точка Кюри керамики ЦТС-19 (около 305К) позволяла припаивать стержни к пьезоэлементу сплавом (висмут-50%, кадмий-25%, олово-25%), имеющим температуру плавления около 105 °С. В [103] отмечается, что отражение от слоев, связывающих отдельные элементы датчика, толщина которых не превышает 0,4 мм, составляет не более 1%. Существенное отражение вызывает пузыри воздуха, поэтому их необходимо тщательно устранять. Стержни с пьезоэлементом должны быть установлены в стенке ударной трубы так, чтобы свести к минимуму акустической контакт между стержнями и стенкой. Поэтому к стержням с помощью эпоксидной смолы крепились кольца из вакуумной резины, затем стержни с пьезоэлементом и кольцами из резины помещались в латунный корпус так, чтобы первый стержень выступал из корпуса на 5 мм, а после этого пространство между кольцами и корпусом заполнялось эпоксидной смолой. Изготовленный таким способом датчик устанавливался в стенке ударной трубы так, чтобы торец первого латунного стержня совпадал с внутренней поверхностью канала трубы, а между стенкой и боковой поверхностью стержня оставался зазор около 0,2 мм. Этот зазор предотвращает акустический контакт между свободным концом первого стержня и стенкой ударной трубы. В противном случае датчик давления регистрирует сигнал, связанный с ударом о стенку ударной трубы лепестков раскрывающейся диафрагмы. Этот сигнал может определить ударную волну или придти почти одновременно с ней и исказить полезный сигнал.
Необходимо подчеркнуть, что первый стержень играет принципиальную роль в конструкции датчика давления. Измерения тепловых потоков показали, что последние в условиях мощных ударных волн могут достигнуть 109 вт/м2. При воздействии теплового потока такой величины в течение 25 мкс средняя температура первого латунного стержня изменится на величину, не превышающую 0,5°. Изменение температуры стержня около пьезокерамики будет еще меньше, следовательно, влиянием этого изменения температуры на пьезоэлемент можно пренебречь. При непосредственном контакте пьезоэлемента с плазмой температура слоя пьезокерамики, лежащего в непосредственной близости от той поверхности пьезоэлемента, которая находится в контакте с плазмой, может достигнуть нескольких сотен градусов. В этом случае пьезоэлемент либо совсем выйдет из строя, либо его свойства будет изменяться от опыта к опыту, т.е. датчик без первого стержня, защищающего пьезоэлемент от непосредственного воздействия плазмы, не может быть использован для количественных исследований. Нужно отметить еще один эффект, который делает применение первого стержня весьма существенным. Как показали предварительные исследования, во время прохождения ударной волны мимо торца датчика давления на стержне возникает электрический сигнал, происхождение которого может быть связано как с электризацией трением или аккомодацией поверхностью датчика свободных зарядов из плазмы, так и с собственным электромагнитным излучением плазмы. Заземление первого стержня позволяет ликвидировать этот сигнал, искажающий осциллограмму давления.
Для датчика, имеющего размеры указанные выше, постоянная времени равна примерно 0,4 мкс, время запаздывания сигнала - около 4,5 мкс, время, в течение которого сигнал не искажен волной упругих напряжений, отраженной от торца второго стержня, не менее 300 мкс.
Один из вариантов крепления датчика давления в стенке ударной трубы показан на рис.7.15. Здесь 1 - пьезоэлемент, 2,3 - латунные стержни, 4 - кольца из вакуумной резины и эпоксидная смола; 5 - латунный корпус; 6 - центрирующее кольцо из тефлона; 7 - болт; 8 - фланец.
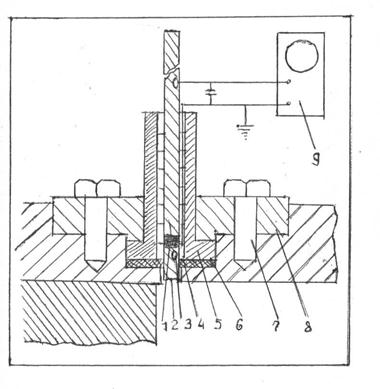
Рис. 7.15.
Особенность регистрации сигнала, возникшего в электрической цепи датчика, обусловлена весьма высоким сопротивлением датчика (более 1010-1012 ом). Зависимость напряжения на входе регистрирующего прибора от времени связана с постоянной времени (RС) электрической цепи между прибором и датчиком давления. В общем случае сопротивление этой цепи определяется сопротивлением датчика, входным сопротивлением регистрирующего прибора, а также сопротивлением утечки подводящих кабелей. При регистрации с помощью осциллографа это сопротивление фактически равно входному сопротивлению осциллографа (500 кОм), т.к. это сопротивление на несколько порядков меньше остальных. Емкость электрической цепи определяется емкостью датчика (~20пкф), емкостью кабеля (~100пкф) и входной емкостью осциллографа (~30пкф). Все эти емкости одного порядка, поэтому замена, например, одного кабеля на другой может повлечь за собой заметное изменение емкости всей цепи. Это обстоятельство влечет за собой необходимость включения параллельно входному сопротивлению осциллографа дополнительной емкости, величина которой должна быть много больше 150пкф. Таким образом, электрическую схему регистрации сигнала можно представить в виде, изображенном на рис.7.16. Здесь обозначено:
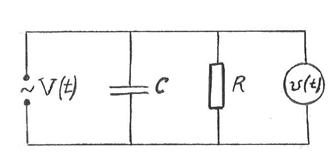
Рис. 7.16
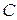 - емкость цепи,
- емкость цепи, 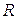 - сопротивление (по существу это входное сопротивление осциллографа).
- сопротивление (по существу это входное сопротивление осциллографа).  и
и  - соответственно напряжения на обкладках пьезоэлемента и зарегистрированное осциллографом.
- соответственно напряжения на обкладках пьезоэлемента и зарегистрированное осциллографом.
Исходя из этой схемы, можно написать:
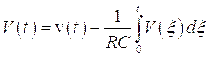 (7.24)
(7.24)
Для оценки, положим  постоянной и равной
постоянной и равной 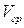 - среднему значению
- среднему значению 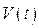 . В этом случае из (7.24) следует:
. В этом случае из (7.24) следует:
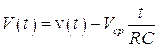 (7.25)
(7.25)
Для того, чтобы можно было считать 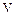 (t)=
(t)= (t) нужно, чтобы
(t) нужно, чтобы 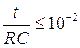 . Отсюда, полагая время регистрации равным 250 мкс, получим
. Отсюда, полагая время регистрации равным 250 мкс, получим  мкф. При прочих равных условиях сигнал будет тем меньше, чем больше
мкф. При прочих равных условиях сигнал будет тем меньше, чем больше  , т.е. увеличение емкости сверх необходимого нецелесообразно. Поэтому величина дополнительной емкости была взята равной 0,05мкф.
, т.е. увеличение емкости сверх необходимого нецелесообразно. Поэтому величина дополнительной емкости была взята равной 0,05мкф.
Тарировку датчика давления в абсолютных единицах целесообразно выполнять в условиях, близких к тем, в которых проводятся измерения. В этом случае можно исключить влияние амплитудно-частотной характеристики датчика давления на результаты изменений. Для этой цели были использованы ударные волны с небольшими числами Маха, т.е. такими, когда нет оснований подвергать сомнению расчетные значения давления, полученные с помощью законов сохранения. Тарировка датчиков осуществлялась с помощью отраженных ударных волн в аргоне, при начальном давлении в камере низкого давления от 50 мм рт. ст. до 1 атм. Для тарировки использовались только такие режимы работы ударной трубы, при которых температура в аргоне за отраженной ударной волной не превышала 8000К, и ионизация аргона исчезающе мала. Высокие значения давления, развивающегося за ударными волнами в этом случае, позволяют пренебречь ролью релаксационных явлений.
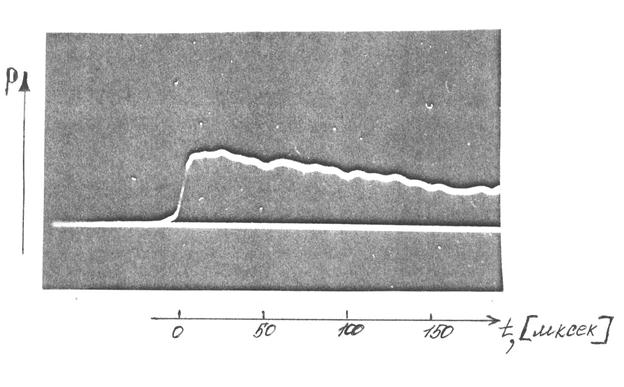
Рис. 7.17.
На рис.7.17 представлена типичная осциллограмма импульса давления в аргоне за отраженной ударной волной. Время нарастания сигнала составляет несколько мкс. Это время в первом приближении равно времени прохождения ударной волной воспринимающей поверхности датчика. Медленное уменьшение амплитуды сигнала обусловлено, по-видимому, уменьшением давления после прохождения ударной волны. На вершине импульса, приведенного на рис.7.17,. видны колебания с периодом, превышающим период собственных колебаний пьезоэлемента. Эти колебания, по-видимому, связаны с колебаниями, обусловленными недостаточно мягкой подвеской пьезоэлемента и латунных стержней. При изменении амплитуды эти колебания усреднялись. Величина сигнала в вольтах определялась путем сравнения амплитуды осциллограммы давления с величиной калибровочного сигнала генератора, который фотографировался на ту же пленку после опыта при неизмененном коэффициенте усиления осциллографа.
В качестве иллюстрации на рис.7.18 приведены результаты измерений давления в двуокиси углерода, которые были выполнены за отраженными ударными волнами в двухдиафрагменной ударной трубе (диаметр внутреннего канала 100 мм).

Рис. 7.18.
На рис.7.18 даны значения давления, отвечающие тем участкам, где его можно считать постоянным обозначения: 0 - при начальном давлении 10 мм.рт.ст. 0 - при начальном давлении 1 мм.рт.ст. Кривыми даны результаты расчета по законам сохранения с учетом диссоциации и ионизации среды за ударными волнами. Резюмируя результаты измерений давления в углекислом газе можно считать установленным для чисел Маха падающей волны, не превышающих 30 и давлений не выше 80 атм, что в течение не менее 20 мксек давление за отраженными ударными волнами отвечает значениям, рассчитанным по законам сохранения.
Аналогичные результаты были получены в случае аргона и воздуха [104].






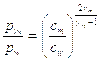
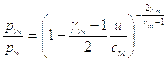
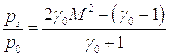
 (7.1)
(7.1)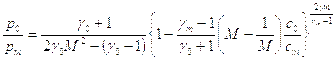
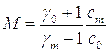 (7.2)
(7.2)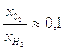 можно получить выигрыш в скорости звука по сравнению с водородом согласно [68] примерно в 1,7 раза. Ту часть водорода, которая не участвует в реакции (~ 70 %), можно заменить гелием. Кислородо-водородо-геливая смесь (КВГС): 1O2 + 2Н2 +7Не практически столь же эффективно повышает скорость ударной волны, как и смесь 1O2 + 9Н2 [61], а соображения безопасности делают более предпочтительным применение КВГС. Согласно [61] наибольшие скорости ударной волны получаются в том случае, когда давление, при котором разрушается диафрагма, примерно в два раза меньше, чем давление, развивающиеся при полном сгорании КВГС в замкнутом сосуде.
можно получить выигрыш в скорости звука по сравнению с водородом согласно [68] примерно в 1,7 раза. Ту часть водорода, которая не участвует в реакции (~ 70 %), можно заменить гелием. Кислородо-водородо-геливая смесь (КВГС): 1O2 + 2Н2 +7Не практически столь же эффективно повышает скорость ударной волны, как и смесь 1O2 + 9Н2 [61], а соображения безопасности делают более предпочтительным применение КВГС. Согласно [61] наибольшие скорости ударной волны получаются в том случае, когда давление, при котором разрушается диафрагма, примерно в два раза меньше, чем давление, развивающиеся при полном сгорании КВГС в замкнутом сосуде.



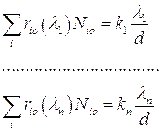 (7.3)
(7.3) (7.4)
(7.4) (7.5)
(7.5) (7.6)
(7.6)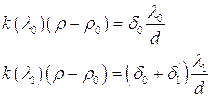 (7.7)
(7.7)![]() – соответственно плотности перед и за ударной волной.
– соответственно плотности перед и за ударной волной.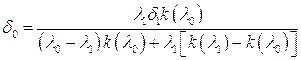 (7.8)
(7.8)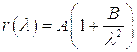 (7.9)
(7.9) ![]() . Воспользовавшись этим, можно показать, что
. Воспользовавшись этим, можно показать, что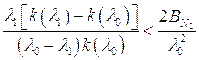 (7.10)
(7.10)![]() ,
, ![]() , т.е. вместо (7.8) можно принять:
, т.е. вместо (7.8) можно принять: (7.11)
(7.11)![]() до целого числа, с помощью первого из уравнений (7.7) можно найти плотность воздуха и за ударной волной.
до целого числа, с помощью первого из уравнений (7.7) можно найти плотность воздуха и за ударной волной. 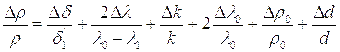 (7.12)
(7.12)![]() может составлять 1%÷5%; положив
может составлять 1%÷5%; положив ![]() , найдем, что величина второго слагаемого может составлять 1%-5%;
, найдем, что величина второго слагаемого может составлять 1%-5%; ![]() не превышает, как это следует из таблицы 2 – 9%; сумма последних трех слагаемых не превышает 1,5%. Необходимо иметь в виду, что при небольших значениях числа Маха,
не превышает, как это следует из таблицы 2 – 9%; сумма последних трех слагаемых не превышает 1,5%. Необходимо иметь в виду, что при небольших значениях числа Маха, ![]() невелико и поэтому сумма первых двух слагаемых может достигать 10%, однако
невелико и поэтому сумма первых двух слагаемых может достигать 10%, однако ![]() в этом случае не превышает 1% - 2%. При числах Маха 20-25 сумма первых двух слагаемых уменьшается до 2%, однако отклонение константы Гладстона – Дейла от значения, принятого в расчетах, как это следует из табл. 7.1. может достигнуть 9% и носит систематический характер.
в этом случае не превышает 1% - 2%. При числах Маха 20-25 сумма первых двух слагаемых уменьшается до 2%, однако отклонение константы Гладстона – Дейла от значения, принятого в расчетах, как это следует из табл. 7.1. может достигнуть 9% и носит систематический характер.

 (7.13)
(7.13)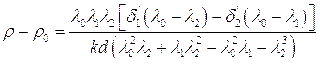 (7.14)
(7.14)


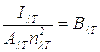 (7.15)
(7.15)
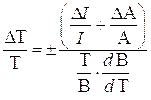 (7.18)
(7.18)


 (7.21)
(7.21)

 :
:
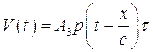
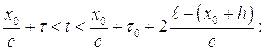
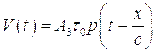
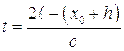 за ходом давления Р(t) с запаздыванием
за ходом давления Р(t) с запаздыванием 

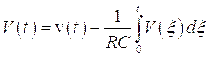 (7.24)
(7.24)


