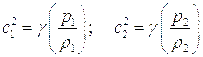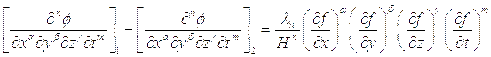ЧАСТЬ II.
Физическая газодинамика.
В первой части книги были рассмотрены движения несжимаемой сплошной среды/ Возникающие в такой среде тангенциальные разрывы скорости приводят к образованию вихрей, т.е. к преобразованию одного типа видимого движения - потенциального в другой тип видимого движения- вихревое; преобразование видимого движения в тепловое, если и имеет место, то в такой степени, что изменения физико-химических параметров среды несущественны. Иной характер имеют нормальные разрывы, возникающие в сжимаемых средах. Перейдем к изучению таких сред.
ГЛАВА V.
Возникновение ударных разрывов.
§1. Нестационарное одномерное течение газа.
Рассмотрим движение сплошной среды, в которой отсутствуют источники (стоки) массы и тепла  , а изменением ее внутренней энергии можно пренебречь
, а изменением ее внутренней энергии можно пренебречь 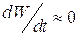 . В этом случае, как показано в §2, гл.I, уравнения (1.6) и (1.7) принимают идентичный вид:
. В этом случае, как показано в §2, гл.I, уравнения (1.6) и (1.7) принимают идентичный вид:
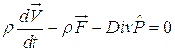
В отличие от задач, рассмотренных в первой части, будем считать, что среда может испытывать сжатие, т.е. уравнение неразрывности имеет вид:

Для простоты ограничимся рассмотрением одномерного движения, происходящего в направлении перпендикулярном направлению объемных сил. Это позволяет отвлечься от вихревых движений в жидкости и основное внимание уделить эффектам, обусловленным сжимаемостью среды. Система уравнений, описывающая движение такой среды примет вид:
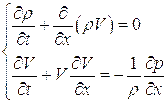 (5.1)
(5.1)
где  - скалярная величина, а ось Ох совпадает с направлением движения жидкости.
- скалярная величина, а ось Ох совпадает с направлением движения жидкости.
Пуассон [26] нашел решение этой системы уравнений для изотермического течения в виде простой волны:
 (5.2)
(5.2)
где 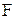 - произвольная функция.
- произвольная функция.
Нетрудно видеть, что в случае изотермического течения  , следовательно,
, следовательно, 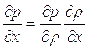 и полагая
и полагая 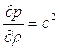 можно системе уравнений (5.1) придать вид:
можно системе уравнений (5.1) придать вид:
 (5.3)
(5.3)
отсюда:
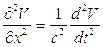 (5.4)
(5.4)
Решение этого уравнения:
 ,
,
поскольку

Подставляя эти соотношения в (5.4), убеждаемся, что оно обращается в тождество. Чэллис [27] обратил внимание на то, что уравнение (5.2), полученное Пуассоном, не всегда имеет единственное решение. В этом нетрудно убедиться, продифференцировав обе части уравнения (5.2) по 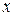 :
:

Если 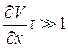 , то это равенство выполняется при любых
, то это равенство выполняется при любых 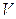 .
.
Стокс [28] предложил считать, что скорость терпит разрыв, если 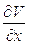 становится бесконечно большой; во всех же остальных областях скорость - однозначная непрерывная функция. К аналогичному выводу пришел и Ирншоу [29]. Вместе с тем Стокс считал, что реально разрывы не существуют, поскольку их возникновению препятствуют силы вязкости. В действительности же наличие сил вязкости приводит лишь к тому, что разрывы не локализуются на бесконечно тонких поверхностях, а имеют конечные размеры.
становится бесконечно большой; во всех же остальных областях скорость - однозначная непрерывная функция. К аналогичному выводу пришел и Ирншоу [29]. Вместе с тем Стокс считал, что реально разрывы не существуют, поскольку их возникновению препятствуют силы вязкости. В действительности же наличие сил вязкости приводит лишь к тому, что разрывы не локализуются на бесконечно тонких поверхностях, а имеют конечные размеры.
Риман [30], полагая течение изотермическим, придал системе уравнений (5.1) вид
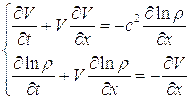 (5.5)
(5.5)
Обозначим:

и введем новые переменные:

В случае идеального газа последние соотношения принимают простой вид:
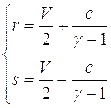
Найдем:
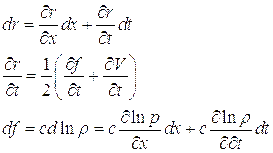
отсюда:
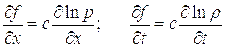
следовательно:
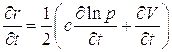
Воспользовавшись (5.5) получим:

Таким образом
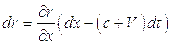
Аналогичные выкладки можно выполнить и для переменной 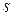 , в результате вместо (5.5) можно записать
, в результате вместо (5.5) можно записать
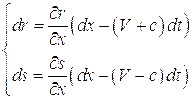 (5.6)
(5.6)
Из этих соотношений следует, что величины  и
и 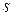 , которые обычно именуют инвариантами Римана, сохраняют свои значения постоянными вдоль линий, отвечающих соответственно условиям:
, которые обычно именуют инвариантами Римана, сохраняют свои значения постоянными вдоль линий, отвечающих соответственно условиям:
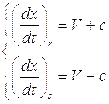 (5.7)
(5.7)
Обозначим эти два семейства кривых, называющиеся характеристиками, соответственно 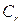 и
и 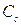 . Совокупность таких линий образуют в плоскости
. Совокупность таких линий образуют в плоскости  сетку кривых, которая может быть построена в явном виде, если проинтегрирована система уравнений (5.6) и найдены функции
сетку кривых, которая может быть построена в явном виде, если проинтегрирована система уравнений (5.6) и найдены функции 
Отметим, что при одномерном движении вдоль оси абсцисс, точке с координатой 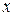 соответствует плоскость, перпендикулярная этой оси, поэтому полученный результат можно интерпретировать, например, как распространение по трубе двух семейств плоских волн в противоположные стороны. Поскольку процесс изоэнтропический, то
соответствует плоскость, перпендикулярная этой оси, поэтому полученный результат можно интерпретировать, например, как распространение по трубе двух семейств плоских волн в противоположные стороны. Поскольку процесс изоэнтропический, то
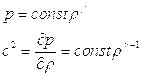
т.е. скорость распространения возмущений тем больше, чем больше плотность. Отсюда следует, что при движении по трубе постоянной скоростью  газа, плотность которого в направлении движения убывает, абсолютная скорость распространения возмущений
газа, плотность которого в направлении движения убывает, абсолютная скорость распространения возмущений  тем больше, чем больше плотность, а следовательно слои с большей плотностью в конце концов должны перегнать слои с меньшей плотностью, а тогда одному и тому же значению абсциссы должно соответствовать более одного значения плотности. Поскольку это невозможно, то последнее означает, что сделанное при выводе дифференциальных уравнений допущение, состоящее в том, что
тем больше, чем больше плотность, а следовательно слои с большей плотностью в конце концов должны перегнать слои с меньшей плотностью, а тогда одному и тому же значению абсциссы должно соответствовать более одного значения плотности. Поскольку это невозможно, то последнее означает, что сделанное при выводе дифференциальных уравнений допущение, состоящее в том, что  и их производные есть непрерывные функции от
и их производные есть непрерывные функции от 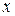 , нарушается, т.е. эти функции в некоторой точке терпят разрыв. Этот вывод аналогичен выводу, следующему из решения Пуассона (5.2), о том, что в движущейся сплошной среде при определенных условиях возникают разрывы ее параметров.
, нарушается, т.е. эти функции в некоторой точке терпят разрыв. Этот вывод аналогичен выводу, следующему из решения Пуассона (5.2), о том, что в движущейся сплошной среде при определенных условиях возникают разрывы ее параметров.
§2. Простые волны. Метод характеристик.
Воспользуемся тем, что
 (5.8)
(5.8)
Выберем для определенности пределы интегрирования в формуле для вычисления 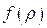 так, чтобы константа в правой части, например, второго из этих уравнений, обратилась в нуль, тогда
так, чтобы константа в правой части, например, второго из этих уравнений, обратилась в нуль, тогда
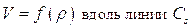
Из определения функции 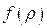 следует, что это соотношение справедливо во всей области течения в любой момент времени, а первое уравнение (5.8) позволяет заключить, что волны семейства
следует, что это соотношение справедливо во всей области течения в любой момент времени, а первое уравнение (5.8) позволяет заключить, что волны семейства 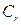 несут постоянные значения скорости
несут постоянные значения скорости  , но тогда можно утверждать, что постоянными здесь будут и значения
, но тогда можно утверждать, что постоянными здесь будут и значения 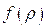 , а следовательно и значения параметров среды плотности, давления и скорости
, а следовательно и значения параметров среды плотности, давления и скорости  . Волны, которые несут постоянные значения параметров газа, называют простыми, т.е. волна, распространяющаяся вдоль характеристики
. Волны, которые несут постоянные значения параметров газа, называют простыми, т.е. волна, распространяющаяся вдоль характеристики  ,-простая
,-простая
Направим ось абсцисс вдоль по потоку, тогда  , это будет означать, что волны семейства
, это будет означать, что волны семейства  распространяются в том же направлении, что и газ, а волны семейства
распространяются в том же направлении, что и газ, а волны семейства 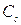 - в противоположную сторону. Поскольку
- в противоположную сторону. Поскольку  , то на основании равенства
, то на основании равенства
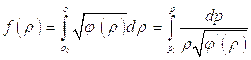 (5.9)
(5.9)
заключаем, что  ,т.е. возмущения, переносимые семейства
,т.е. возмущения, переносимые семейства 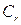 сжимают газ и их можно считать волнами сжатия.
сжимают газ и их можно считать волнами сжатия.
Поступим аналогично, выбрав постоянную интегрирования при вычислении 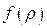 таким образом, чтобы константа в выражении
таким образом, чтобы константа в выражении

обратилась в нуль, тогда найдем, что скорость 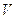 постоянна вдоль линий семейства
постоянна вдоль линий семейства  , а следовательно сохраняет свое значение
, а следовательно сохраняет свое значение  , а значит остаются постоянными и величины давления, плотности и скорости
, а значит остаются постоянными и величины давления, плотности и скорости 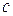 , т.е. волны семейства
, т.е. волны семейства 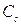 также являются совокупностью простых волн, распространяющихся в сторону обратную движению газа. На основании предыдущего равенства можно утверждать, что
также являются совокупностью простых волн, распространяющихся в сторону обратную движению газа. На основании предыдущего равенства можно утверждать, что  , а воспользовавшись соотношением (5.9) приходим к выводу, что волны семейства
, а воспользовавшись соотношением (5.9) приходим к выводу, что волны семейства  представляют собой волны разрежения.
представляют собой волны разрежения.
С помощью равенств (5.7) можно построить графоаналитический способ решения системы уравнений (5.6) в изоэнтропическом случае, если вдоль некоторой кривой 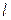 , не являющейся характеристикой, задано распределение скорости
, не являющейся характеристикой, задано распределение скорости 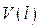 и параметров среды
и параметров среды 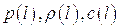 , а следовательно и инвариантов Римана.
, а следовательно и инвариантов Римана.
В этом случае можно определить угловые коэффициенты характеристик 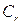 и
и 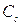 в точках М и N (рис.5.1) по формулам (5.7) и построить
в точках М и N (рис.5.1) по формулам (5.7) и построить 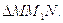
На отрезке 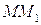 характеристики
характеристики  остается постоянным инвариант
остается постоянным инвариант 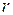 , следовательно
, следовательно
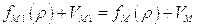

Рис. 5.1.
а на отрезке 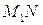 характеристики
характеристики 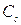 -значение инварианта
-значение инварианта  :
:
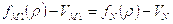
Из двух последних равенств можно найти:
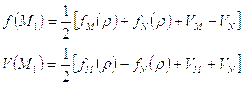
а, следовательно, и 
Аналогично можно определить значения параметров среды в точке 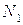 и т.д. Поскольку точки
и т.д. Поскольку точки  и т.д. на кривой
и т.д. на кривой 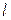 могут быть взяты сколь угодно близко друг к другу, то значения
могут быть взяты сколь угодно близко друг к другу, то значения  могут быть найдены в любой точке плоскости
могут быть найдены в любой точке плоскости  , а, следовательно, и решена поставленная задача
, а, следовательно, и решена поставленная задача
§3. Распространение звука.
Звуковыми волнами называют периодические движения малой амплитуды, обусловленные сжатием среды. Уравнение распространения плоских звуковых волн можно получить, продифференцировав первое из уравнений системы (5.2) по времени, а второе по координате; исключив после этого слагаемые содержащие 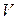 , будем иметь:
, будем иметь:

Полагая
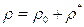
где  - среднее значение плотности,
- среднее значение плотности,
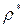 - малые отклонения от среднего, преобразуем это уравнение к виду:
- малые отклонения от среднего, преобразуем это уравнение к виду:
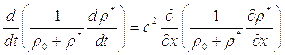
Отсюда, с учетом того, что  , следует:
, следует:

Поскольку
 ,
,
то для покоящейся среды 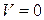 , имеем:
, имеем:
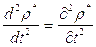
В результате, для описания распространения малых возмущений плотности, получим волновое уравнение:
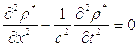 (5.10)
(5.10)
Воспользовавшись тем, что
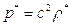
где 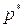 - возмущения давления среды, обусловленные возмущениями плотности, можно получить для распространения возмущения давления уравнение, аналогичное (5.10):
- возмущения давления среды, обусловленные возмущениями плотности, можно получить для распространения возмущения давления уравнение, аналогичное (5.10):

Рассмотрим решение уравнения (5.10) и с этой целью введем новые переменные:

тогда:
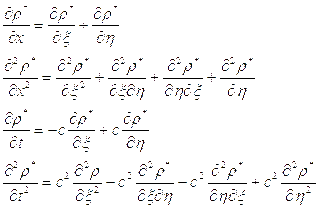
Подставляя эти выражения в исходное уравнение, получим:
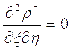
После интегрирования по  , получим:
, получим:

где 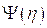 - произвольная функция.
- произвольная функция.
После интегрирования этого уравнения по 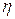 будем иметь:
будем иметь:
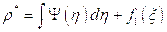
или
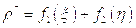
где 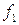 и
и 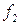 - произвольные функции, следовательно
- произвольные функции, следовательно

Аналогичной формулой описываются в этом случае и плотность и давление.
Преобразование координат, сделанное выше, имеет простой кинематический смысл. Ось координат 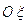 располагается вдоль оси Ох и движется поступательно в положительном направлении этой оси со скоростью
располагается вдоль оси Ох и движется поступательно в положительном направлении этой оси со скоростью 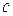 , а ось
, а ось  движется поступательно в обратном направлении. Функция
движется поступательно в обратном направлении. Функция  представляет собой не зависящее от времени распределение плотности или давления в подвижной системе координат
представляет собой не зависящее от времени распределение плотности или давления в подвижной системе координат 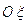 . Эта фиксированная форма распределения плотности или давления, заданная его начальным распределением перемещается как целое в положительном направлении оси Ох. Аналогично функция
. Эта фиксированная форма распределения плотности или давления, заданная его начальным распределением перемещается как целое в положительном направлении оси Ох. Аналогично функция 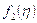 дает фиксированную форму распределения плотности или давления, распространяющуюся в обратном по отношению к оси Ох направлении. Для наглядности положим
дает фиксированную форму распределения плотности или давления, распространяющуюся в обратном по отношению к оси Ох направлении. Для наглядности положим 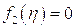 . В каждой плоскости
. В каждой плоскости  давление, также как и плотность, изменяются со временем, принимая одни и те же значения в любой точке плоскости, поскольку
давление, также как и плотность, изменяются со временем, принимая одни и те же значения в любой точке плоскости, поскольку 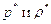 не зависят от координат
не зависят от координат  . Вместе с тем
. Вместе с тем 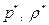 одинаковы в плоскости, отвечающей условию
одинаковы в плоскости, отвечающей условию 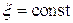 , т.е. одинаковы для всех точек плоскости, отвечающих условию
, т.е. одинаковы для всех точек плоскости, отвечающих условию 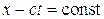 . Следовательно, если в начальный момент
. Следовательно, если в начальный момент 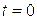 в некоторой плоскости параметры жидкости имеют определенные значения, то через некоторый интервал времени
в некоторой плоскости параметры жидкости имеют определенные значения, то через некоторый интервал времени 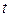 , те же самые значения параметры принимают на плоскости, находящейся от первоначального положения на расстоянии
, те же самые значения параметры принимают на плоскости, находящейся от первоначального положения на расстоянии  вдоль оси Ох. Плоскость с заданными параметрами среды перемещается в пространстве со скоростью
вдоль оси Ох. Плоскость с заданными параметрами среды перемещается в пространстве со скоростью 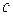 . Этот процесс принято называть распространением плоской бегущей волны, а величину
. Этот процесс принято называть распространением плоской бегущей волны, а величину  - скоростью распространения волны. Таким образом, будут иметь место две системы плоских волн, отвечающие условиям:
- скоростью распространения волны. Таким образом, будут иметь место две системы плоских волн, отвечающие условиям:
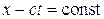 и
и 
которые представляют собой две распространяющиеся в противоположные стороны со скоростью  перпендикулярные оси Ох плоскости, на каждой из которых сохраняются заданные исходными условиями значения давления и плотности среды, т.е. звуковые волны являются простыми.
перпендикулярные оси Ох плоскости, на каждой из которых сохраняются заданные исходными условиями значения давления и плотности среды, т.е. звуковые волны являются простыми.
Полученному решению можно дать геометрическую интерпретацию, состоящую в том, что в плоскости 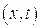 имеют место два семейства прямых
имеют место два семейства прямых  с угловыми коэффициентами
с угловыми коэффициентами  , вдоль каждой из которых сохраняются постоянными заданные начальными условиями параметры среды. Эти два семейства прямых представляют собой два семейства характеристик волнового уравнения.
, вдоль каждой из которых сохраняются постоянными заданные начальными условиями параметры среды. Эти два семейства прямых представляют собой два семейства характеристик волнового уравнения.
Скорость распространения простых волн называют скоростью распространения малых возмущений в сплошной среде. Если среда движется, то величина

представляет собой скорость распространения малых возмущений относительно движущейся среды, т.е. местную скорость распространения малых возмущений в данной точке потока.
Распространение звука представляет собой типичный случай распространения малых возмущений. В плоской волне отлична от нуля только компонента 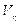 , т.е. скорость среды в плоской звуковой волне направлена вдоль ее распространения, поэтому звуковые волны являются волнами продольными. При распространении звуковых волн в газе существенное значение имеет характер процесса распространения звука. Ньютон предлагал считать этот процесс изотермическим, т.е.
, т.е. скорость среды в плоской звуковой волне направлена вдоль ее распространения, поэтому звуковые волны являются волнами продольными. При распространении звуковых волн в газе существенное значение имеет характер процесса распространения звука. Ньютон предлагал считать этот процесс изотермическим, т.е.  , где
, где 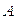 - константа.
- константа.
В этом случае:
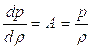
т.е. изотермическая скорость звука
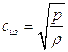
Лаплас полагал, что при распространении звука сжатие газа происходит очень быстро, а, следовательно, потерями тепла можно пренебречь и считать процесс адиабатическим, т.е. 
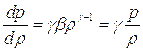
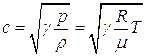
где  - отношение теплоемкости газа при постоянном давлении к теплоемкости при постоянном объеме,
- отношение теплоемкости газа при постоянном давлении к теплоемкости при постоянном объеме,  - константа,
- константа,
 - молекулярный вес газа,
- молекулярный вес газа,
 - универсальная газовая постоянная.
- универсальная газовая постоянная.
Экспериментальные данные свидетельствуют о том, что распространение звука происходит адиабатически. Отметим также, что скорость звука и тепловая скорость молекул в газе - величины одного порядка.
Рассмотрим поведение сферической звуковой волны, т.е. такой волны, параметры которой зависят только от расстояния от некоторого центра. В этом случае распределение параметров в волне должно обладать сферической симметрией, а значит, в волновом уравнении можно положить равным нулю производные по угловым координатам. Волновое уравнение, например, для давления будет иметь вид

С помощью подстановки:
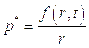
Уравнению можно придать вид:

Это уравнение отличается от рассмотренного выше только тем, что роль координаты играет не  , а
, а 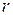 . Решение его имеет вид:
. Решение его имеет вид:
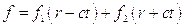
где 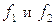 -произвольные функции.
-произвольные функции.
Следовательно, решением волнового уравнения в случае сферической симметрии будет:

где первое слагаемое отражает распространение волны, расходящейся во все стороны от начала координат, а второе представляет собой волну, сходящуюся к центру.
Отметим, что в случае плоской волны амплитуда остается постоянной, тогда как в сферической волне амплитуда уменьшается обратно пропорционально расстоянию от центра. Интенсивность волны пропорциональна квадрату амплитуды, а это означает, что интенсивность волны убывает обратно пропорционально квадрату расстояния от начала координат
Предположим, что в начале координат нет источника звука, тогда давление при  должно быть конечным, а для этого необходимо, чтобы
должно быть конечным, а для этого необходимо, чтобы  , а, следовательно, имеет место сферическая стоячая волна:
, а, следовательно, имеет место сферическая стоячая волна:

Если в начале координат расположен источник, то должна иметь место расходящаяся волна  , а поскольку решение относится только к области вне тела, то отпадает и требование конечности значений давлений при
, а поскольку решение относится только к области вне тела, то отпадает и требование конечности значений давлений при 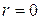 .
.
Если функция 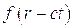 имеет периодический характер, то ее можно разложить в ряд Фурье:
имеет периодический характер, то ее можно разложить в ряд Фурье:
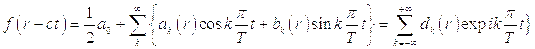
где
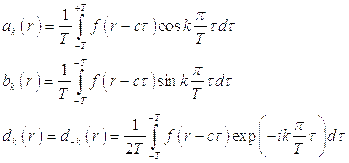
 - полупериод функции
- полупериод функции 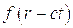
В этом случае звуковую волну можно рассматривать, как совокупность гармонических волн, каждая из которых отвечает определенной частоте: 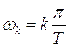 . Если длина гармонической волны
. Если длина гармонической волны 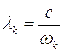 пренебрежимо мала по сравнению с характерным масштабом задачи, то такие задачи относят к геометрической акустике, методы решения задач которой аналогичны методам геометрической оптики.
пренебрежимо мала по сравнению с характерным масштабом задачи, то такие задачи относят к геометрической акустике, методы решения задач которой аналогичны методам геометрической оптики.
Поскольку звуковая волна является простой волной, то для нее справедливы результаты, полученные в предыдущем параграфе для простой волны. В частности, на основании этих результатов можно утверждать, что по истечении достаточно большого интервала времени на протяжении каждого ее периода должен возникнуть разрыв. Конечно, это заключение относится к звуковой волне достаточно большой амплитуды, поскольку в противном случае звуковая волна может затухнуть за счет вязкости и теплопроводности прежде, чем в ней возникнут разрывы. Отметим, что гармоническая звуковая волна за счет возникновения разрывов, а, следовательно, за счет существенного изменения своего профиля, перестает быть таковой. Последнее означает, что при разложении в ряд Фурье профиля волны, бывшей ранее гармонической, будут иметь место наряду с основной гармоникой и обертоны с частотами кратными основной.
§4. Истечение сжимаемого газа из сосуда большой емкости.
Рассмотрим стационарное истечение совершенного газа из сосуда настолько большого объема, что изменением давления в нем за счет истечения можно пренебречь. Если условия истечения таковы, что поток можно считать одномерным, то, воспользовавшись (5.1), получим:
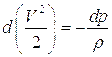
Или, интегрируя вдоль элементарной струйки:

Здесь: 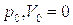 -давление и скорость газа в сосуде;
-давление и скорость газа в сосуде;
 - давление, скорость и плотность газа в данном сечении элементарной струйки.
- давление, скорость и плотность газа в данном сечении элементарной струйки.
Будем считать, что истечение происходит адиабатически, т.е.

тогда с помощью предыдущего соотношения получим:

Если размеры отверстия, как вдоль, так и поперек струи, достаточно малы, то на основании этого соотношения можно утверждать, что при неограниченном увеличении давления в сосуде скорость истечения достигает значения равного местной скорости звука. Скорость потока газа равная местной скорости звука называется критической -  , соответствующие этому состоянию значения давления, плотности и температуры -
, соответствующие этому состоянию значения давления, плотности и температуры - 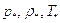 также называются критическими.
также называются критическими.
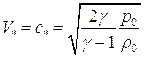
Этой скорости соответствует соответствует критическое давление:
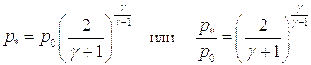
Это отношение для воздуха составляет примерно 0,53. Масса газа, истекающего в единицу времени из отверстия сечения 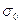 , можно вычислить согласно:
, можно вычислить согласно:

Сен-Венан обратил внимание на то, что расход газа, если бы эта формула была справедлива для любого значения давления в открытом пространстве 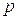 , должен был бы с уменьшением
, должен был бы с уменьшением 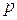 возрастать от нуля при
возрастать от нуля при 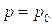 , проходить через максимум и затем снова обращаться в нуль при
, проходить через максимум и затем снова обращаться в нуль при  . Значение давления
. Значение давления  , соответствующее максимуму расхода можно найти из условия
, соответствующее максимуму расхода можно найти из условия

откуда:
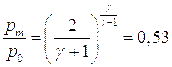
следовательно: 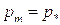
Гюгенио высказал предположение, что в том случае, когда 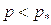 , истекающая струя газа разделяется поверхностью, на которой скорость потока равна скорости звука, на две части, причем давление при переходе через эту поверхность терпит разрыв, таким образом, что выше по потоку от этой поверхности оно равно 0.53
, истекающая струя газа разделяется поверхностью, на которой скорость потока равна скорости звука, на две части, причем давление при переходе через эту поверхность терпит разрыв, таким образом, что выше по потоку от этой поверхности оно равно 0.53 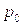 , а ниже оно равно давлению в открытом пространстве. В этом случае в отверстии устанавливается скорость истечения равная скорости звука и расход становится независящим от давления в открытом пространстве. После выхода из отверстия струя газа расширяется, причем за счет инерции настолько сильно, что давление в ней становится меньше давления в открытом пространстве. Это обстоятельство приводит к тому, что истекающая струя перестает расширяться и начинает сжиматься пока давление внутри нее не станет близким давлению в открытом пространстве, затем этот процесс повторяется снова. Возникает периодическая структура [5]. Для того чтобы достигнуть сверхзвуковой скорости истечения, канал, соединяющий объем с открытым пространством, профилируют-делают сначала суживающимся, а затем расширяющимся специальным образом (сопло Лаваля).
, а ниже оно равно давлению в открытом пространстве. В этом случае в отверстии устанавливается скорость истечения равная скорости звука и расход становится независящим от давления в открытом пространстве. После выхода из отверстия струя газа расширяется, причем за счет инерции настолько сильно, что давление в ней становится меньше давления в открытом пространстве. Это обстоятельство приводит к тому, что истекающая струя перестает расширяться и начинает сжиматься пока давление внутри нее не станет близким давлению в открытом пространстве, затем этот процесс повторяется снова. Возникает периодическая структура [5]. Для того чтобы достигнуть сверхзвуковой скорости истечения, канал, соединяющий объем с открытым пространством, профилируют-делают сначала суживающимся, а затем расширяющимся специальным образом (сопло Лаваля).
§5. Ударная адиабата.
Предыдущее рассмотрение показывает, что движение сжимаемой среды сопровождается возникновением разрывов ее параметров. Первые экспериментальные исследования разрывов были выполнены в связи с изучением процессов горения и детонации: за рубежом - Бертело [31,32], Малларом и Ле-Шателье [33], Виэем [34], в России - Михельсоном [35]. Окончательное становление теории разрывных течений связано с именами Рэнкина [36] и Гюгонио [37]
Рассмотрим основные принципы, лежащие в основе теории распространения разрывов сплошных сред. Будем считать разрыв сильным, если терпят разрыв непосредственно параметры среды; если же терпят разрыв их производные, то будем называть разрыв слабым. Термин разрыв порядка «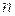 » означает, что на данной поверхности, по крайней мере, одна из производных порядка «
» означает, что на данной поверхности, по крайней мере, одна из производных порядка «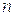 » терпит разрыв, тогда как все производные порядков меньших «
» терпит разрыв, тогда как все производные порядков меньших «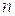 », остаются непрерывными. Сторону разрыва, обращенную в направлении движения среды, будем именовать передним фронтом.
», остаются непрерывными. Сторону разрыва, обращенную в направлении движения среды, будем именовать передним фронтом.
В качестве исходных принципов воспользуемся общими теоремами динамики, записанными в интегральной форме (гл.I, §1). Рассмотрим одномерный случай, что позволяет упростить задачу, исключив вихревые движения среды. Направим ось абсцисс вдоль нормали к поверхности разрыва. Запишем общие теоремы динамики для столба газа, образующая боковой поверхности которого параллельна оси абсцисс, а разрыв располагается между основаниями цилиндра. Обозначим координаты оснований  ,
,  и координату фронта
и координату фронта  , а его скорость соответственно
, а его скорость соответственно 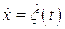 . В этом случае уравнение (1.3) обращается в тождество, а уравнениям (1.1;1.2;1.4) можно придать вид:
. В этом случае уравнение (1.3) обращается в тождество, а уравнениям (1.1;1.2;1.4) можно придать вид:
 (5.11)
(5.11)
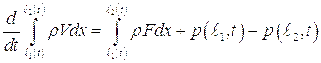 (5.12)
(5.12)
 (5.13)
(5.13)
здесь: 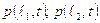 - значения давления на основаниях столба газа.
- значения давления на основаниях столба газа.
Интегралы, стоящие в левых частях этих уравнений, относятся к интегралам вида:
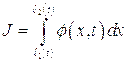
где подынтегральная функция терпит разрыв в точке  внутри интервала
внутри интервала 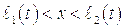
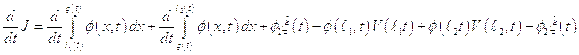 (5.14)
(5.14)
здесь  и
и  - пределы функции
- пределы функции  , когда
, когда  приближается к
приближается к 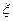 соответственно со стороны
соответственно со стороны 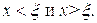
Положение оснований цилиндра и, соответственно, его длина при выводе этой формулы были выбраны произвольно. Будем неограниченно уменьшать длину цилиндра, но так, чтобы передний фронт разрыва располагался между его основаниями. Поскольку передний фронт представляет собой поверхность, то высота цилиндра может быть сделана столь угодно малой, а, следовательно, и сколь угодно малым значение интеграла в правой части формулы (5.14), при этом значение  стремится к
стремится к 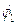 , а
, а 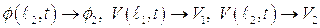 , следовательно
, следовательно
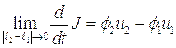
где  - есть скорости течения слева и справа от переднего фронта, в системе координат, связанной с ним. В этом случае интегралы, стоящие в правых частях уравнений (5.11-5.13), также стремятся к нулю. В результате эти уравнения принимают вид:
- есть скорости течения слева и справа от переднего фронта, в системе координат, связанной с ним. В этом случае интегралы, стоящие в правых частях уравнений (5.11-5.13), также стремятся к нулю. В результате эти уравнения принимают вид:
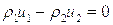 (5.15)
(5.15)
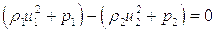 (5.16)
(5.16)
 (5.17)
(5.17)
здесь индексами 1 и 2 отмечены параметры среды до и после разрыва соответственно. Совокупность этих уравнений называют динамическими условиями совместимости движений среды до и после разрыва. В соответствии с принципом относительности Галилея эти уравнения инвариантны относительно движения системы отсчета с постоянной скоростью.
Система уравнений (5.15-5.17) допускает тривиальное решение:  . В этом случае (5.15) и (5.17) удовлетворяются автоматически, а из (5.16) следует
. В этом случае (5.15) и (5.17) удовлетворяются автоматически, а из (5.16) следует 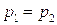 . Разрывы, отвечающие этому условию, относят к тангенциальным разрывам и называют контактными поверхностями. Отметим, что контактная поверхность неустойчивое образование, размывающаяся со временем в некоторую область [38].
. Разрывы, отвечающие этому условию, относят к тангенциальным разрывам и называют контактными поверхностями. Отметим, что контактная поверхность неустойчивое образование, размывающаяся со временем в некоторую область [38].
Разрывы, соответствующие нетривиальным решениям (5.15-5.17), именуют ударными волнами. За ширину ударной волны примем расстояние от ее переднего фронта до того места, где установилось локальное термодинамическое равновесие, т.е. состояние при котором имеет место равновесие между внутренними степенями свободы среды, однако равновесия излучения с веществом может и не быть.
Уравнения (5.15-5.17) не позволяют определить направление распространения разрыва, т.к. они симметричны по отношению к обеим состояниям. Для устранения этой неопределенности систему уравнений (5.15-5.17) необходимо дополнить требованием возрастания энтропии. Для того, чтобы эта система уравнений стала замкнутой, т.е. позволяла найти параметры состояния среды по одну сторону разрыва, если известны его скорость и параметры состояния среды по другую его сторону, необходимо к системе уравнений (5.15-5.17) присоединить соотношения, связывающие внутреннюю энергию с параметрами, определяющими состояние среды до и после переднего фронта.
В случае локального термодинамического равновесия внутренняя энергия есть однозначная функция термодинамических параметров. При отсутствии равновесия она зависит еще от параметров, характеризующих возбуждение внутренних степей свободы. В этом случае к уравнениям (5.15-5.17), необходимо добавить соотношение, связывающее внутреннюю энергию не только с давлением и плотностью, но и с параметрами - 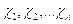 , характеризующими возбуждение внутренних степей свободы среды. Кроме того, должны быть известны значения этих параметров непосредственно за передним фронтом, а также уравнения, описывающие поведение этих параметров во времени:
, характеризующими возбуждение внутренних степей свободы среды. Кроме того, должны быть известны значения этих параметров непосредственно за передним фронтом, а также уравнения, описывающие поведение этих параметров во времени:
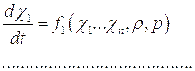

Большинство авторов исходят из модели, согласно которой непосредственно за передним фронтом ударной волны на расстоянии порядка длины свободного пробега устанавливается больцмановское распределение молекул газа по поступательным степеням свободы. Обмен энергией между поступательными и внутренними степенями свободы молекул (колебательными и электронными), а также процессы диссоциации и ионизации протекают существенно медленнее, чем процесс установления больцмановского распределения молекул по поступательным степеням свободы. Это обстоятельство позволяет вычислять значения внутренней энергии газа непосредственно за передним фронтом ударной волны, считая газ совершенным с неизменным отношением теплоемкостей при постоянном давлении и постоянном объеме. После этого можно с помощью уравнений (5.15-5.17) и уравнения состояния найти значения плотности и давления. Далее задавшись уравнениями, описывающими поведение параметров 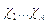 и уравнениями движения в интегральной или дифференциальной форме можно описать поведение среды в последующие моменты времени.
и уравнениями движения в интегральной или дифференциальной форме можно описать поведение среды в последующие моменты времени.
Весьма важным для практики является случай, когда локальное термодинамическое равновесие устанавливается за передним фронтом настолько быстро, что толщиной ударной волны можно пренебречь и считать ее поверхностью. Уравнения (5.15 – 5.17) в этом случае остаются в силе. Вместе с уравнением состояния они образуют замкнутую систему уравнений, которая позволяет найти значения термодинамических параметров среды за ударной волной, если известны ее скорость и значение термодинамических параметров перед ней. Уравнения (5.15 – 5.17) в случае ударной волны бесконечно малой толщины, можно переписать в виде:
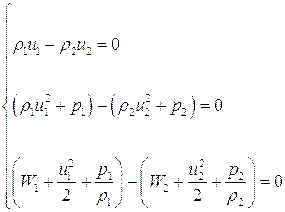 (5.18)
(5.18)
Заменив внутреннюю энергию энтальпией, согласно  , последнему уравнению этой системы можно придать вид:
, последнему уравнению этой системы можно придать вид:
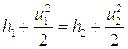 (5.19)
(5.19)
Из первых двух уравнений этой системы следует:
 (5.20)
(5.20)
Подставив эти выражения в последнее уравнение (5.18) и в (5.19) получим:
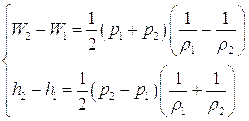 (5.21)
(5.21)
Поскольку эти соотношения связывают начальные и конечные значения давления и плотности, то по аналогии с адиабатой Пуассона от этих соотношениях говорят, как об адиабате Гюгонио или ударной адиабате.
Найдем связь между скоростями до и после скачка уплотнения 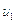 и
и 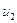 . С этой целью перепишем первые два уравнения системы (5.18) в виде:
. С этой целью перепишем первые два уравнения системы (5.18) в виде:
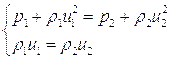
Поделив почленно первое из этих уравнений на второе, получим:
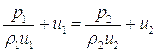
или
 (5.22)
(5.22)
Исключим из этого уравнения  и
и 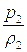 . С этой целью запишем уравнение (1.7) для случая адиабатического движения
. С этой целью запишем уравнение (1.7) для случая адиабатического движения 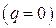 идеального газа
идеального газа 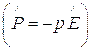
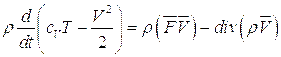
Связь между внутренней энергией и энтальпией с учетом того, что
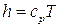

можно представить в виде:

С помощью этих соотношений уравнение баланса энергии преобразуем к виду:
 (5.23)
(5.23)
Последнему слагаемому в правой части этого уравнения, вычислив производную и воспользовавшись уравнением неразрывности в виде:
 ,
,
придадим вид:
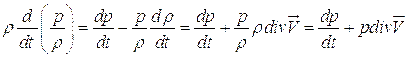
Подставляя это выражение в (5.23):
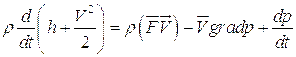
и учитывая, что
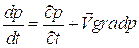
получим:
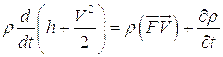 (5.24)
(5.24)
Если движение стационарно, а объемные силы консервативны, то:
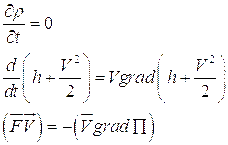
В этом случае равенство (5.24) преобразуется к виду:
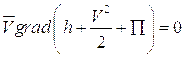
Если можно считать объемные силы независящими от координат, т.е. 

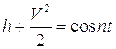
Поскольку
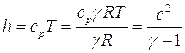
то последнему уравнению можно придать вид:

Постоянную величину в этом уравнении можно определить либо, полагая  при
при  , тогда
, тогда

либо полагая 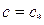 , при
, при 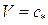 , где
, где  - критическая скорость, тогда
- критическая скорость, тогда
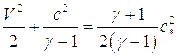 (5.25)
(5.25)
отметим также, что

откуда
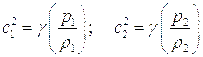
Записав уравнение (5.25) с учетом этих соотношений для скоростей газа до и после ударной волны 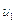 и
и 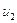 , получим:
, получим:

Заменив с помощью этих соотношений  и
и 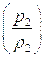 в уравнении (5.22), получим:
в уравнении (5.22), получим:

следовательно:
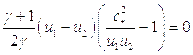
поскольку 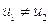 , то отсюда следует формула Прандтля, связывающая скорости газа до и после фронта ударной волны с критической скоростью:
, то отсюда следует формула Прандтля, связывающая скорости газа до и после фронта ударной волны с критической скоростью:
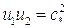 (5.26)
(5.26)
Необходимо также иметь в виду, что существование поверхности разрыва в данный момент, а также в течение конечного интервала времени, влечет за собой выполнение соответственно тождественных и кинематических условий совместимости установленных Гюгонио [37]. В формулировке Адамара [39] эти условия могут быть записаны в таком виде [40]:
тождественные условия –

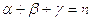
кинематические условия –
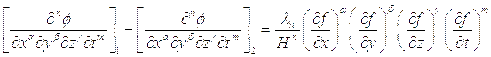

здесь:
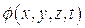 – смещение среды,
– смещение среды,
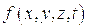 – поверхность волнового фронта,
– поверхность волнового фронта,
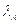 - произвольная постоянная,
- произвольная постоянная,
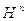 - первый дифференциальный параметр от поверхности волнового фронта, индексами 1 и 2 помечены величины, относящиеся к областям, лежащим, соответственно, до и после разрыва.
- первый дифференциальный параметр от поверхности волнового фронта, индексами 1 и 2 помечены величины, относящиеся к областям, лежащим, соответственно, до и после разрыва.




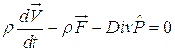
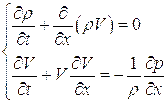 (5.1)
(5.1) (5.3)
(5.3)
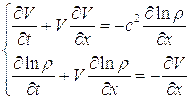 (5.5)
(5.5)

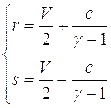
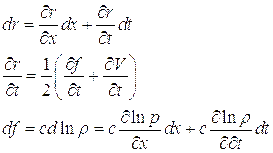
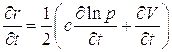

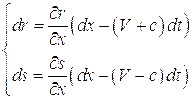 (5.6)
(5.6)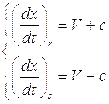 (5.7)
(5.7)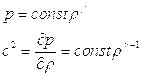
 (5.8)
(5.8)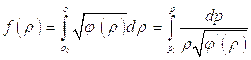 (5.9)
(5.9)
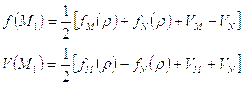
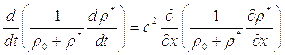
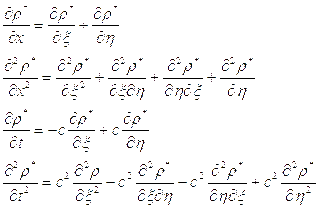

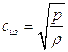
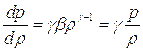
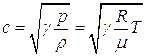

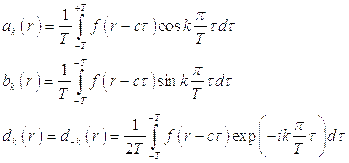
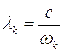 пренебрежимо мала по сравнению с характерным масштабом задачи, то такие задачи относят к геометрической акустике, методы решения задач которой аналогичны методам геометрической оптики.
пренебрежимо мала по сравнению с характерным масштабом задачи, то такие задачи относят к геометрической акустике, методы решения задач которой аналогичны методам геометрической оптики. 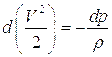



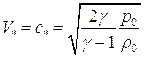
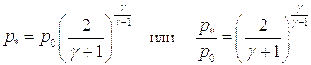


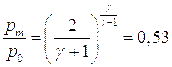
 (5.11)
(5.11)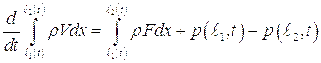 (5.12)
(5.12) (5.13)
(5.13)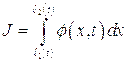
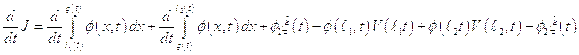 (5.14)
(5.14) (5.17)
(5.17)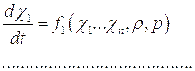
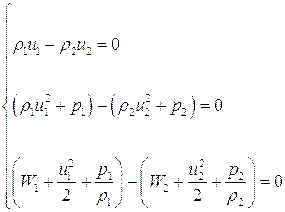 (5.18)
(5.18) , последнему уравнению этой системы можно придать вид:
, последнему уравнению этой системы можно придать вид: (5.20)
(5.20)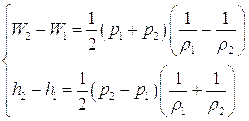 (5.21)
(5.21)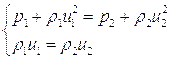
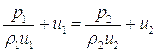
 (5.22)
(5.22)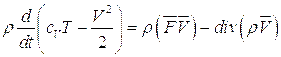

 (5.23)
(5.23)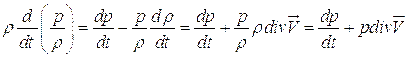
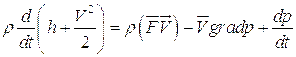
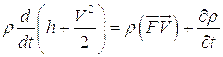 (5.24)
(5.24)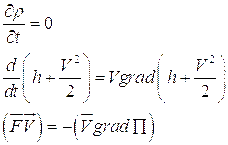
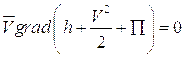
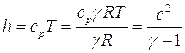


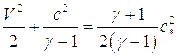 (5.25)
(5.25)