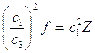ГЛАВА IV.
Общее уравнение поля в электродинамике и квантовой механике.
Коллективное взаимодействие частей системы гидромеханической природы может быть описано, как это следует из предыдущей главы с помощью общего уравнения поля. Целесообразно рассмотреть возможность распространения такого подхода на взаимодействие электромагнитного характера.
§1. Распространение электромагнитных возмущений и общее уравнение поля.
Физические явления обусловлены двумя принципиально отличными друг от друга способами передачи сигналов. Один совершается с помощью тел, имеющих массу, и происходит со скоростью их движения, второй – путем распространения возмущений в сплошной среде и совершается с групповой скоростью инициированных ими волн. В главе I показано, что система уравнений, являющаяся следствием законов сохранения массы, количества движения и энергии для случая среды, не содержащей разрывов, должна быть дополнена уравнением, описывающим способ обмена сигналами между частями механической системы. В том случае, когда обмен совершается с помощью механических сигналов, таким условием служит гипотеза, предложенная [15], которая вместе с законами сохранения приводит к системе уравнений (3.6.). Если элементы системы несут электрический заряд, то наряду с механическим взаимодействием имеет место и взаимодействие электромагнитной природы, которое описывается системой уравнений Максвелла:


здесь: 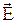 ,
, 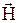 – векторы напряженности электрического и магнитного поля;
– векторы напряженности электрического и магнитного поля;
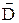 – вектор электрического смещения;
– вектор электрического смещения;
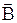 - вектор магнитной индукции;
- вектор магнитной индукции;
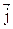 - вектор плотности электрического тока;
- вектор плотности электрического тока;
 - объемная плотность свободных зарядов;
- объемная плотность свободных зарядов;
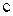 - скорость распространения электромагнитных возмущений в вакууме.
- скорость распространения электромагнитных возмущений в вакууме.
Эти уравнения обычно дополняют соотношениями, характеризующими свойства среды и связывающими 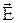 и
и  ,
, 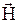 и
и 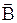 ,
,  и
и 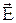 , которые имеют вид:
, которые имеют вид:
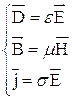
здесь: 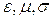 - диэлектрическая и магнитная проницаемость и проводимость среды соответственно.
- диэлектрическая и магнитная проницаемость и проводимость среды соответственно.
Если воспользоваться этими соотношениями, то в случае отсутствия избыточных зарядов и токов, происходящих от действия сторонних электродвижущих сил, уравнениям Максвелла можно придать вид:
 (4.1)
(4.1)
Если исключить отсюда вектор  , то для вектора
, то для вектора 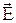 получим уравнение:
получим уравнение:
 (4.2)
(4.2)
Исключив из системы уравнений (4.1) вектор 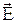 получим уравнение для
получим уравнение для  , имеющее идентичный вид. Нетрудно показать, что такой же вид будут иметь уравнения для скалярного
, имеющее идентичный вид. Нетрудно показать, что такой же вид будут иметь уравнения для скалярного  и векторного потенциалов
и векторного потенциалов  электромагнитного поля. Если ввести вектор
электромагнитного поля. Если ввести вектор 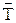 – поляризационный потенциал, удовлетворяющий уравнению:
– поляризационный потенциал, удовлетворяющий уравнению:
 (4.3)
(4.3)
где 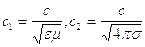 , то уравнения (4.1) выполняются, если положить.
, то уравнения (4.1) выполняются, если положить.
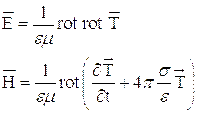
Отметим, что вектор  совпадает с вектором Герца для непроводящей среды, т.е. при
совпадает с вектором Герца для непроводящей среды, т.е. при  = 0.
= 0.
Из изложенного ясно, что поведение характеристик электромагнитного поля описывается уравнением типа (3.5). Отличие состоит лишь в том, что в случае электромагнитного поля следует положить
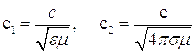
Это обстоятельство служит дополнительным аргументом в пользу того, чтобы называть уравнение (3.5) общим уравнением поля.
Отметим, что в случае вакуума, т.е. в тех областях пространства, где отсутствуют частицы вещества уравнение (4.3) приобретает вид:
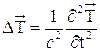 (4.4)
(4.4)
Покажем, что это уравнение инвариантно по отношению к преобразованиям Лоренца. Пусть сходственные оси декартовых прямоугольных систем координат 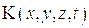 и
и 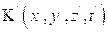 параллельны и система
параллельны и система  движется относительно системы К с постоянной скоростью
движется относительно системы К с постоянной скоростью  направленной вдоль оси Ox, причем в момент начала отчета времени t и t’ начала координат обеих систем совпадают, тогда преобразования Лоренца имеют вид:
направленной вдоль оси Ox, причем в момент начала отчета времени t и t’ начала координат обеих систем совпадают, тогда преобразования Лоренца имеют вид:
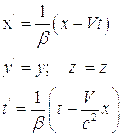
где 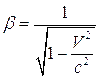
Произведем с помощью этих соотношений замену переменных в исходном уравнении
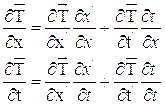
поскольку

то

После этого найдем значения вторых производных:
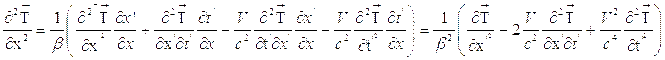


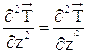
Подставляя эти выражения в (4.4) получим:

откуда:
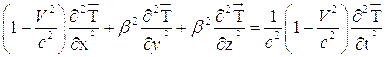
или

Отсюда следует, что уравнение (4.4) инвариантно по отношению к преобразованиям Лоренца, причем отметим, что проведенное рассмотрение
справедливо, если скорость распространения электромагнитных возмущений “c” в обеих системах  и
и  одинакова, т.е. не зависит от скорости их движения, поэтому постоянство скорости света в вакууме следует рассматривать не как аксиому, а как следствие принципа относительности.
одинакова, т.е. не зависит от скорости их движения, поэтому постоянство скорости света в вакууме следует рассматривать не как аксиому, а как следствие принципа относительности.
Посредником, ответственным за распространение электромагнитных возмущений следует считать вакуум, т.е. объект в котором отсутствуют материальные тела, но вместе с тем могут распространяться возмущения силовых полей. Для вакуума не существует понятий движения или покоя, аналогично тому, как невозможно движения «ничего» относительно «ничего». Процессы распространения возмущений силовых полей в вакууме и движения материальных сред в нем независимы, поэтому в соответствии с опытом Майкельсона скорость распространения возмущения силовых полей не может никоим образом зависеть от скорости распространения возмущений поля параметров материальной среды. Вместе с тем можно утверждать, что распространение возмущений силовых полей в вакууме и распространение возмущений в несжимаемой изотермической материальной среде обладает некоторыми общими признаками, которые и находят отражение в общем уравнении поля. Изложенный подход коррелирует с точкой зрения Эйнштейна [22]: “… пространство немыслимо без эфира, действительно в таком пространстве не только было бы невозможно распространение света, но и не могли бы существовать масштабы и часы и не было бы никаких пространственных расстояний в физическом смысле слова. Однако этот эфир нельзя представить себе состоящим из прослеживаемых во времени частей; таким свойством обладает только весомая материя; точно также к нему нельзя применять понятие движения”.
Рассмотрим, в качестве примера, распространение электромагнитных возмущений в неограниченной среде на расстояниях достаточно больших от источника таких, что электромагнитное поле можно считать сферически симметричным, т.е. его компоненты зависят только от расстояния до источника возмущений. Расположим сферическую систему координат таким образом, чтобы ее центр совпадал с источником возмущений. В этом случае вектор скорости распространения возмущений будет направлен вдоль радиуса, а векторы электрической и магнитной напряженности образуют с ним правую тройку. Вектор электрической напряженности:
Поскольку  ,
,
то  , где
, где  функция от
функция от 
Уравнению (4.2) с помощью соотношений (3.28) можно придать вид:
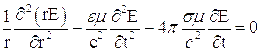 (4.5)
(4.5)
причем функция  должна отвечать условиям:
должна отвечать условиям:
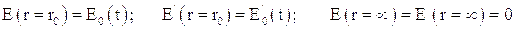
здесь 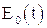 - значение электрической напряженности на расстоянии от источника, настолько большом, чтобы электромагнитное поле можно было считать сферически симметричным; известная функция от времени.
- значение электрической напряженности на расстоянии от источника, настолько большом, чтобы электромагнитное поле можно было считать сферически симметричным; известная функция от времени.
Если 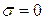 , то последнее уравнение принимает вид волнового уравнения:
, то последнее уравнение принимает вид волнового уравнения:
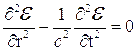
где 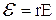
Нетрудно видеть, что общим решением этого уравнения будет
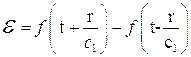
следовательно
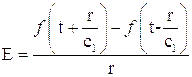
Вид функции 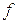 определяется исходными условиями (подробнее см. напр. [20]).
определяется исходными условиями (подробнее см. напр. [20]).
В случае установившегося периодического процесса функцию  можно разложить в ряд Фурье:
можно разложить в ряд Фурье: 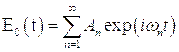 и решение уравнения (4.5) целесообразно искать в виде:
и решение уравнения (4.5) целесообразно искать в виде:

Для компонента  с помощью (4.5) получим
с помощью (4.5) получим

откуда для 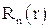 следует:
следует:
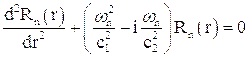
или

где
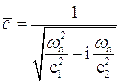
можно интерпретировать как комплексную скорость, причем ее действительную часть можно интерпретировать, как скорость распространения возмущения, а мнимую как показатель поглощения.
§2. Уравнение Шредингера и общее уравнение поля.
В атомных системах возмущения силовых полей обусловлены движением частиц, имеющих массу, поэтому для описания таких систем необходимо использовать оба уравнения (3.6). Поскольку распределение массы в атомных системах неоднородно, то, проинтегрировав первое из уравнений (3.6) по пространству, найдем, что члены нового уравнения, содержащие плотность, отличны от нуля только в границах электрона, а интеграл от поверхностных сил обращается в нуль. Общее уравнение поля можно записать для вектора поляризационного потенциала(4.3) или для векторов напряженности электрического(4.2) и магнитного поля, которые имеют идентичный вид.
В том случае, когда объемные силы имеют потенциал, система уравнений, описывающая поведение атомной системы, может быть представлена в виде:
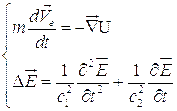 (4.6)
(4.6)
где 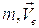 - масса и скорость электрона,
- масса и скорость электрона,
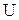 - потенциальная энергия.
- потенциальная энергия.
Для вектора напряженности магнитного поля 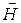 справедливо уравнение идентичное уравнению для напряженности электрического поля
справедливо уравнение идентичное уравнению для напряженности электрического поля 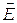 .
.
Будем задавать положение электрона расстоянием  , пройденным им вдоль траектории, тогда
, пройденным им вдоль траектории, тогда
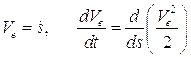
C помощью этих соотношений после интегрирования первого уравнения системы (4.6) нетрудно получить

или
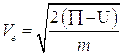
где 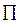 - значение энергии в той точке, где потенциальная энергия U=0. Поскольку электромагнитные возмущения в атомной системе порождены движением электрона, то следует считать, что групповая скорость распространения пакета возмущений электромагнитного поля близка скорости движения электрона. Положение волнового пакета определяется его максимумом, для которого справедливо
- значение энергии в той точке, где потенциальная энергия U=0. Поскольку электромагнитные возмущения в атомной системе порождены движением электрона, то следует считать, что групповая скорость распространения пакета возмущений электромагнитного поля близка скорости движения электрона. Положение волнового пакета определяется его максимумом, для которого справедливо

где 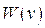 - фазовая скорость распространения возмущений, отсюда
- фазовая скорость распространения возмущений, отсюда

Полагая, что 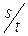 - групповая скорость распространения возмущений равна скорости движения электрона
- групповая скорость распространения возмущений равна скорости движения электрона  , найдем:
, найдем:
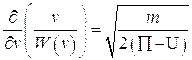
Поскольку в оптике роль функции Гамильтона, т.е. энергии частицы, играет частота, то следует положить
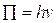 (4.7)
(4.7)
где 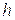 - постоянный коэффициент, и последнее уравнение примет вид:
- постоянный коэффициент, и последнее уравнение примет вид:
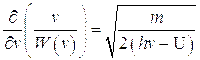
Отсюда после интегрирования следует:
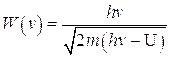
Отождествляя эту величину со скоростью 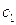 - в общем уравнении поля (4.6), получим:
- в общем уравнении поля (4.6), получим:
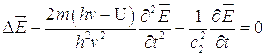
Будем считать, что вектор электрической напряженности можно представить в виде:
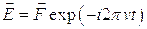 (4.8)
(4.8)
где 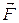 -векторная функция, зависящая только от координат, тогда справедливо
-векторная функция, зависящая только от координат, тогда справедливо
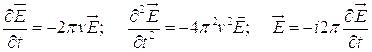
и предыдущему уравнению можно придать вид:
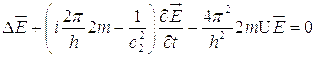 (4.9)
(4.9)
слагаемое, содержащее множитель  , определяет затухание возмущений электрического поля со временем, а конкретизация вида этого множителя обусловлена механизмом диссипации энергии атомной системы. Если эффектами диссипации энергии можно пренебречь, а величину
, определяет затухание возмущений электрического поля со временем, а конкретизация вида этого множителя обусловлена механизмом диссипации энергии атомной системы. Если эффектами диссипации энергии можно пренебречь, а величину  положить равной постоянной Планка, то уравнение (4.9) принимает вид аналогичный уравнению Шредингера:
положить равной постоянной Планка, то уравнение (4.9) принимает вид аналогичный уравнению Шредингера:
 (4.10)
(4.10)
Отличие этого уравнения от уравнения Шредингера состоит в том, что здесь место  - функции занимает вектор электрической (или магнитной) напряженности.
- функции занимает вектор электрической (или магнитной) напряженности.
§3. Гидромеханические аналогии в квантовой механике.
Воспользуемся уравнением (4.10) для решения задач квантовой механики. Стационарные состояния характеризуются постоянным значением энергии, поэтому соотношение (4.8) с учетом (4.7) для случая стационарных состояний можно записать в виде:

и соответственно уравнение (4.10):

здесь обозначено: 
Нетрудно видеть, что уравнение для функции  имеет идентичный вид:
имеет идентичный вид:
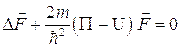 (4.12)
(4.12)
Рассмотрим решение этого уравнения, когда потенциальная энергия имеет вид “потенциальной ямы”

Рис. 4.1
 , если
, если 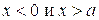
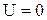 , если
, если 
Положим:
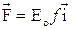
где  - произвольная функция, зависящая только от
- произвольная функция, зависящая только от  ,
,
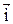 - орт оси ОX,
- орт оси ОX,
 -константа, представляющая собой характерное значение электрической напряженности,
-константа, представляющая собой характерное значение электрической напряженности,
и введем безразмерную координату 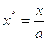 , тогда уравнение (4.12) можно представить в виде
, тогда уравнение (4.12) можно представить в виде
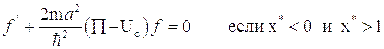

Поскольку для дискретного спектра 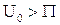 , то вместо этих соотношений можно написать:
, то вместо этих соотношений можно написать:
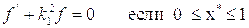

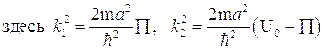
Решение первого уравнения:

Решением второго уравнения с учетом ограниченности его на бесконечности будет:

причем знак «+» относится к области  , знак «-» к области
, знак «-» к области  ,
, 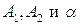 константы, определяющиеся исходными условиями задачи.
константы, определяющиеся исходными условиями задачи.
Поскольку на границах “ямы” напряженность электрического поля и первая ее производная должны быть непрерывны, то выполняются условия

Отсюда:
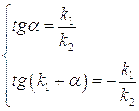
или, исключая 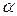 , получим
, получим
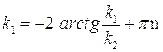
Поскольку это уравнение выполняется лишь для определенных значений 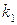 и
и  , а следовательно и
, а следовательно и 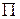 , то отсюда вытекает, что стационарные состояния отвечают лишь дискретным значениям энергии, которые определяются согласно
, то отсюда вытекает, что стационарные состояния отвечают лишь дискретным значениям энергии, которые определяются согласно
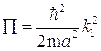
где 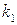 - корень последнего уравнения.
- корень последнего уравнения.
В случае бесконечно глубокой «ямы»  , поэтому
, поэтому  , а следовательно
, а следовательно
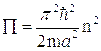
Этот результат аналогичен соотношению, которое следует из решения задачи об обтекании жидкостью прямоугольного канала (§2, Гл. III). В самом деле, на основании решений уравнений (3.10) и (3.14), можно утверждать, что амплитуды отдельных гармоник скорости жидкости пропорциональны 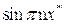 . Полагая кинетическую энергию вихря пропорциональной
. Полагая кинетическую энергию вихря пропорциональной 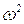 , получим, на основании (3.3), что она, в случае
, получим, на основании (3.3), что она, в случае 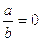 , пропорциональна
, пропорциональна 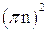 .
.
Аналогия имеет место также между зависимостью напряженности электромагнитного поля ротатора от угловых координат и угловым распределением скоростей при обтекании шара стационарным потоком жидкости. Ротатор представляет собой частицу, свободно движущуюся по сфере постоянного радиуса  . Задача о движении такой частицы является частным случаем задачи о движении в поле центральных сил, когда потенциальную энергию можно считать постоянной. В этом случае целесообразно воспользоваться сферической системой координат, совместив ее начало с центром сферы, и, не ограничивая общности, считать потенциальную энергию равной нулю. По аналогии с рис.3.4, §4, гл.III, положим:
. Задача о движении такой частицы является частным случаем задачи о движении в поле центральных сил, когда потенциальную энергию можно считать постоянной. В этом случае целесообразно воспользоваться сферической системой координат, совместив ее начало с центром сферы, и, не ограничивая общности, считать потенциальную энергию равной нулю. По аналогии с рис.3.4, §4, гл.III, положим:
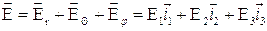
Уравнение (4.11) будет эквивалентно системе из трех уравнений, повторяющих уравнения (3.28), с тем отличием, что в левой их части места 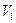 ,
,  и
и 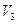 займут
займут 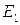 ,
, 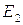 и
и 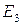 , а в правой части место
, а в правой части место 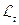 займет
займет  . Выполнив преобразования, аналогичные проведенным в §4, гл.III, получим систему уравнений:
. Выполнив преобразования, аналогичные проведенным в §4, гл.III, получим систему уравнений:
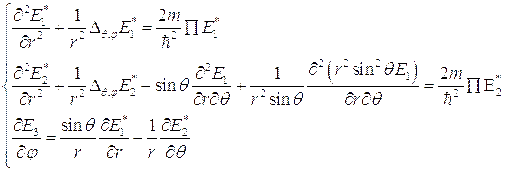
где 
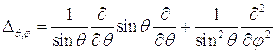
Полагая
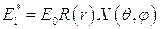
вместо первого уравнения этой системы получим:
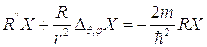
откуда следует:
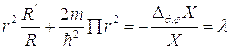
Повторив выкладки §4, гл. III получим, что  , где
, где 
Поскольку в данной задаче 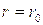 , то
, то 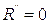 , и из последнего уравнения следует, что энергия может принимать только дискретные значения:
, и из последнего уравнения следует, что энергия может принимать только дискретные значения:
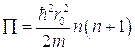
Уравнение
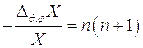
представляет собой уравнение сферических функций, соответствующих значениям  , т.е. угловое распределение компонент электрической напряженности ротатора аналогично зависимости компонент скорости от углов
, т.е. угловое распределение компонент электрической напряженности ротатора аналогично зависимости компонент скорости от углов 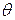 и
и  при обтекании сферы стационарным потоком жидкости.
при обтекании сферы стационарным потоком жидкости.
Уравнение, описывающее поведение резонатора, которое Планк положил в основу его квантовой теории излучения [23]
 (4.13)
(4.13)
где 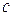 - скорость света в вакууме,
- скорость света в вакууме,  и
и  -параметры резонатора,
-параметры резонатора,
можно рассматривать, как следствие общего уравнения поля.
Если некоторый объем среды, распространение электромагнитных возмущений в которой подчинятся общему уравнению поля, ограничен поверхностью, часть которой - S, находится под воздействием электромагнитного поля с электрической напряженностью Z(t), то электрическое поле в этом объеме описывается уравнением:
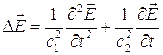
с граничным условием:

Пусть поверхность S представляет собой плоскость, причем вектор  перпендикулярен к ней, тогда вместо векторного уравнения можно ограничиться дифференциальным уравнением, для модуля вектора электрической напряженности. Будем искать решение этого уравнения в виде:
перпендикулярен к ней, тогда вместо векторного уравнения можно ограничиться дифференциальным уравнением, для модуля вектора электрической напряженности. Будем искать решение этого уравнения в виде:

где  - новая неизвестная функция, а функция
- новая неизвестная функция, а функция  подбирается так, чтобы удовлетворялось граничное условие:
подбирается так, чтобы удовлетворялось граничное условие:
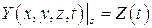
тогда для функции 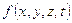 справедливо уравнение
справедливо уравнение

причем 
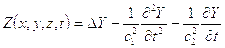
В том случае, когда справедливо:
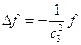
где 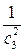 - константа, получим уравнение:
- константа, получим уравнение:
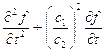 +
+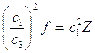
Это уравнение идентично (4.13), если функции, входящие в него можно считать независящими от координат.
Укажем, что параллели в гидромеханике и квантовой механике не ограничиваются отмеченными выше. В [10] показано, что решения уравнения Шредингера находятся в однозначном соответствии с потенциальными течениями обобщенно баротропной жидкости, если функция давления задана специальным образом. Общеизвестно использование нелинейного уравнения Шредингера для описания распространения локализованных пакетов волн на поверхности жидкости [24,25].





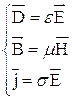
 (4.1)
(4.1) (4.2)
(4.2) (4.3)
(4.3)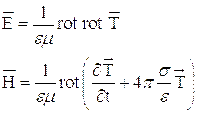
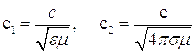
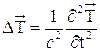 (4.4)
(4.4)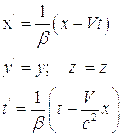
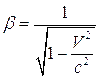
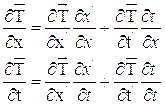


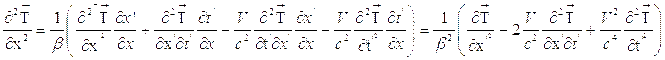


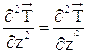

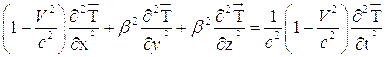

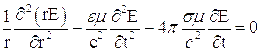 (4.5)
(4.5)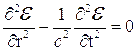
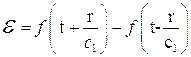
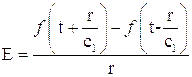
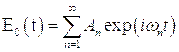 и решение уравнения (4.5) целесообразно искать в виде:
и решение уравнения (4.5) целесообразно искать в виде:

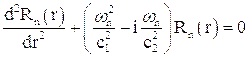
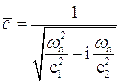
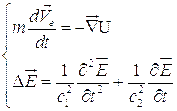 (4.6)
(4.6)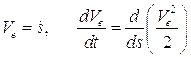
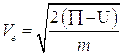


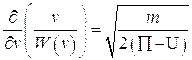
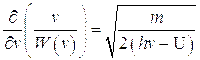
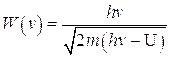
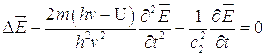
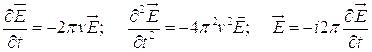
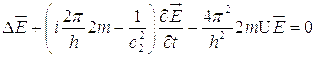 (4.9)
(4.9) (4.10)
(4.10)


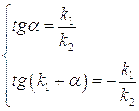
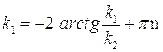
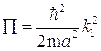
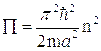
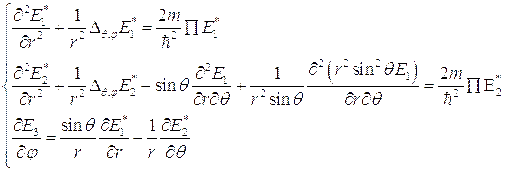
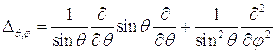
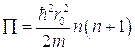
 (4.13)
(4.13)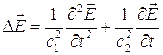

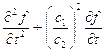 +
+