ГЛАВА II.
Вихревые движения жидкости.
Проведенный анализ уравнений гидродинамики показывает, что их решение существенно зависит от кинематических характеристик течения, поэтому целесообразно более подробно рассмотреть кинематические характеристики движения жидкости.
§1. Движение невязкой жидкости, содержащей вихри.
В общем случае движение твердого тела можно представить состоящим из поступательного со скоростью центра масс и вращательного вокруг мгновенной оси вращения, проходящей через центр масс. Движение жидкой частицы осложняется тем, что наряду с указанными движениями изменяется и ее форма.
Будем считать, что в любой заданный момент движения жидкости разность скоростей двух соседних элементарных ее объемов с точностью до величин первого порядка малости равна вариации скорости, т.е.
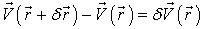
где  - вариация радиуса-вектора центра масс элементарного объема жидкости.
- вариация радиуса-вектора центра масс элементарного объема жидкости.
В этом случае, пользуясь правилами векторного и тензорного анализа [13], найдем:
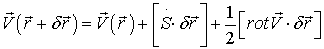
где  - тензор скоростей деформаций.
- тензор скоростей деформаций.
Последнее соотношение позволяет утверждать, что движение элементарного объема жидкости в любой момент времени можно представить состоящим из: а) поступательного движения со скоростью центра масс частицы 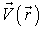 , б) движения, имеющего потенциал скоростей, которое называют деформацией, в) вращения с угловой скоростью
, б) движения, имеющего потенциал скоростей, которое называют деформацией, в) вращения с угловой скоростью

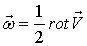 (2.1)
(2.1)
Это утверждение представляет собой так называемую первую теорему Гельмгольца  , которую он сформулировал, опираясь на гидродинамические интегралы Коши
, которую он сформулировал, опираясь на гидродинамические интегралы Коши . Отметим, что Коши сделал разложение движения жидкой частицы на составляющие в несколько иной форме нежели Гельмгольц. Жуковский
. Отметим, что Коши сделал разложение движения жидкой частицы на составляющие в несколько иной форме нежели Гельмгольц. Жуковский  , указывая на дискуссию по этому вопросу между Гельмгольцем и Бертраном, отмечал, что задача об отделении движения деформации от вращения допускает множество различных решений, пока не принята точка зрения Гельмгольца о том, что вращение есть то, что является лишним в движении с потенциалом скоростей. В основу дальнейшего изложения положена эта точка зрения, причем соотношение (2.1) служит определением угловой скорости частицы.
, указывая на дискуссию по этому вопросу между Гельмгольцем и Бертраном, отмечал, что задача об отделении движения деформации от вращения допускает множество различных решений, пока не принята точка зрения Гельмгольца о том, что вращение есть то, что является лишним в движении с потенциалом скоростей. В основу дальнейшего изложения положена эта точка зрения, причем соотношение (2.1) служит определением угловой скорости частицы.
Рассмотрим поле векторов угловых скоростей движущейся жидкости. Назовем вихревой линией такую линию, в каждой точке которой вектор угловой скорости совпадает с касательной к ней. Вихревая поверхность это совокупность вихревых линий, проведенных через некоторый контур. Вихревой нитью будем называть часть жидкости, ограниченную вихревой поверхностью, проведенной через замкнутый контур, причем вихревую нить будем считать элементарной, если контур настолько мал, что в его пределах угловую скорость можно считать постоянной. Величину 
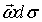 , где
, где 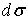 - площадь поперечного сечения элементарной нити, называют напряжением вихря, а величину
- площадь поперечного сечения элементарной нити, называют напряжением вихря, а величину 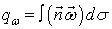 - потоком вектора напряжения вихря сквозь поверхность
- потоком вектора напряжения вихря сквозь поверхность  , причем направление единичного вектора нормали
, причем направление единичного вектора нормали 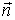 к поверхности
к поверхности  выбрано так, чтобы косинус угла между векторами
выбрано так, чтобы косинус угла между векторами  и
и 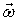 был бы положительным.
был бы положительным.
Докажем вторую теорему Гельмгольца: поток вектора напряжения вихря вдоль вихревой нити постоянен.
Для доказательства запишем теорему Остроградского-Гаусса для потока вектора напряжения вихря через поверхность 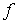 , ограничивающую объем (рис. 2.1)
, ограничивающую объем (рис. 2.1)
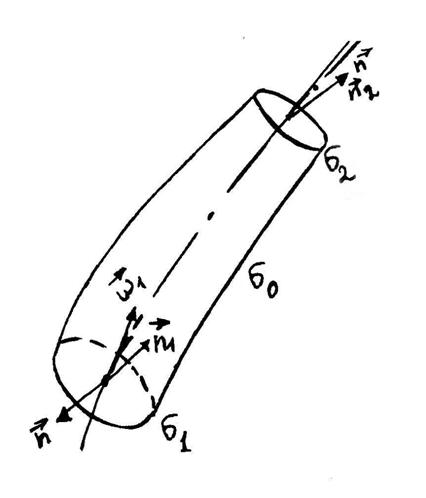
Рис. 2.1
Поверхность, ограничивающая этот объем, представляет собой совокупность трех поверхностей: поверхности вихревой нити с площадью  и поверхностей двух ее произвольных поперечных сечений с площадями -
и поверхностей двух ее произвольных поперечных сечений с площадями - 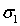 и
и 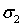 . В этом случае теорема Остроградского-Гаусса принимает вид:
. В этом случае теорема Остроградского-Гаусса принимает вид:

или
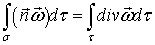
Правая часть этого соотношения равна нулю, а левую часть можно представить в виде суммы трех слагаемых, которые соответствуют трем поверхностям, ограничивающим объем  , в результате получим:
, в результате получим:
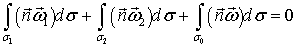
 - поток вектора напряжения вихря сквозь сечение
- поток вектора напряжения вихря сквозь сечение 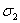 ,
,
 - поток вектора напряжения вихря сквозь сечение
- поток вектора напряжения вихря сквозь сечение  .
.
Таким образом

что и требовалось доказать, поскольку сечения  и
и  выбраны произвольно.
выбраны произвольно.
Докажем важное следствие, вытекающее из второй теоремы Гельмгольца: - вихревые нити не могут заканчиваться нигде внутри объема жидкости; они либо опираются на ограничивающую жидкость поверхности, либо представляют собой замкнутые кольца. В самом деле, на основании второй теоремы Гельмгольца для элементарной вихревой нити, ограниченной плоскими и нормальными к боковой поверхности сечениями 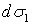 и
и  можно записать
можно записать

Отсюда следует, что сечение нити не может стать равным нулю, поскольку в этом случае угловая скорость вращения жидких частиц в этом сечении должна была бы возрастать до бесконечности.
Теорема Стокса дает наглядное определение потока напряженности вихря с помощью циркуляции вектора скорости: поток вектора напряженности вихревой нити равен половине циркуляции вектора скорости по замкнутому контуру, лежащему на ее поверхности и охватывающему ее один раз. В самом деле:
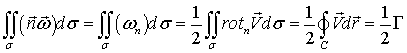 (2.2)
(2.2)
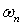 ,
,  - проекции векторов
- проекции векторов 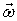 ,
, 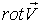 на нормаль к элементарной площадке
на нормаль к элементарной площадке  ,
,  - замкнутый контур, охватывающий площадку площадью
- замкнутый контур, охватывающий площадку площадью  .
.
Рассмотренные теоремы не связаны с какими либо физико-химическими свойствами и отражают общие кинематические закономерности. Важным дополнением к этим теоремам служат теоремы, относящиеся к идеальной жидкости, т.е. жидкости, течение которой отвечает уравнению Эйлера (1.12).
Теорема Кельвина: циркуляция скорости по замкнутому контуру, проводимому через одни и те же частицы в случае движения идеальной жидкости под действием объемных сил с однозначным потенциалом остается неизменной во все времена движения.
С целью доказательства этой теоремы найдем производную по времени от интеграла вдоль произвольной кривой АВ:
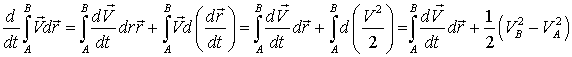
Если точки А и В представляют собой начало и конец замкнутого контура С, то отсюда

Поскольку жидкость идеальна, то на основе уравнения Эйлера (1.12) можно записать:
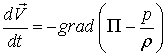
Подставляя это выражение в предыдущие уравнения, получим:
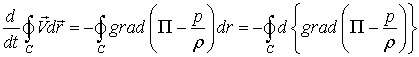
Поскольку потенциальная энергия и давление есть однозначные функции координат, то
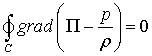
и, следовательно
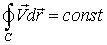
что и требовалось доказать.
Из теоремы Кельвина, как следствие вытекает теорема Лагранжа: если в начальный момент времени течение идеальной жидкости, двигающейся под действием объемных сил с однозначным потенциалом, было безвихревым, то оно останется таковым и в последующие моменты времени.
Для доказательства этой теоремы воспользуемся теоремой Стокса и поскольку половина величины циркуляции скорости по замкнутому контуру равна потоку вектора напряженности вихревой нити, которую он охватывает, то в данном случае можно утверждать, что
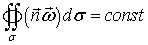
Если в начальный момент времени во всей области течения 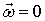 , тогда в любой момент времени справедливо
, тогда в любой момент времени справедливо

Поскольку поверхность  выбрана произвольно, то отсюда следует
выбрана произвольно, то отсюда следует

Причем это равенство справедливо для любого направления 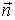 , а значит
, а значит  , что и доказывает теорему Лагранжа.
, что и доказывает теорему Лагранжа.
Для идеальной жидкости, движущейся под действием объемных сил, имеющих однозначный потенциал, кроме доказанных теорем справедливы III и IV теоремы Гельмгольца.
III теорема Гельмгольца: вихревая нить во все время движения остается вихревой нитью.
Для доказательства этой теоремы проведем на боковой поверхности вихревой нити замкнутый контур. Циркуляция скорости по этому контуру в начальный момент времени равна нулю. По теореме Кельина циркуляция по этому контуру при его движении вместе с жидкостью остается равной нулю. Следовательно, ни одна из элементарных вихревых нитей не пересекает ограниченную им поверхность, т.е. характеристики вихревой нити не изменяются, она остается вихревой нитью.
IV теорема Гельмгольца: поток напряженности вихревой нити во время ее движения не изменяется.
Нетрудно видеть, что, охватив заданную вихревую нить замкнутым контуром можно утверждать на основании теоремы Стокса, что поток ее напряженности равен половине циркуляции скорости по этому контуру, а по теореме Кельвина циркуляция скорости остается неизменной, что и доказывает эту теорему.
Суммируя кратко результаты этого раздела можно констатировать, что при движении идеальной жидкости внутри неё вихрей не возникает, а если таковые имели место в начальный момент, то они сохраняют во время движения свои характеристики неизменными. Вместе с тем в природе имеет место взаимодействие вихрей между собой и с поверхностями твердых тел, поэтому целесообразно рассмотреть и эффекты, сопутствующие этим процессам.
§2. Взаимодействие вихревых нитей с окружающей средой.
Рассмотрим движение жидкости внутри и вне неограниченного длинного прямого кругового цилиндра радиуса 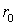 , заполненного совокупностью элементарных вихревых нитей, в плоскости перпендикулярной оси цилиндра (рис. 2.2).
, заполненного совокупностью элементарных вихревых нитей, в плоскости перпендикулярной оси цилиндра (рис. 2.2).

Рис. 2.2
Воспользовавшись соотношением (2.2), интегрируя от 0 до  получим:
получим:
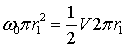
откуда
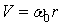 для
для 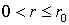
Интегрируя от 0 до 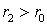 , получим:
, получим:

откуда
 для
для 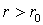
Таким образом, внутри однородного вихря кругового сечения жидкость вращается, как твердое тело с постоянной угловой скоростью; вне такого вихря невихревое движение жидкости совершается так, что площадь, ометаемая в единицу времени радиусом-вектором движущейся частицы, остается постоянной. В случае идеальной невязкой жидкости из предыдущего следует, что такой вихрь будет существовать неограниченно долго, если он имел место в первоначальный момент. Вместе с тем отметим, что такой же вывод следует сделать и в случае вязкой жидкости, если вязкость учитывать согласно уравнению Навье-Стокса, поскольку слагаемое, с помощью которого учитывается диссипация движения за счет трения, обращается в нуль:
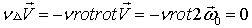
Следовательно, использование этого уравнения для описания цилиндрического вихря приводит к выводу, что такой вихрь не расходует энергии на преодоление сил трения, несмотря на то, что в этом случае 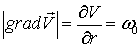 отличен от нуля, а значит отличны от нуля и силы трения.
отличен от нуля, а значит отличны от нуля и силы трения.
Вокруг вихревой линии возникает поле, которое обычно называют индуцированным. В этом случае задача сводится к отысканию такого поля скоростей неограниченной жидкости, в котором скорость уменьшалась бы до нуля при неограниченном удалении от вихревой нити с заданной циркуляцией по контуру, охватывающему нить -  .
.
Введем векторный потенциал  , такой что
, такой что
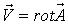
тогда согласно (2.1) можно написать
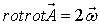
найдем векторный потенциал, отвечающий дополнительному условию:
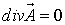
Воспользовавшись формулой векторного анализа:

получим:
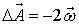
причем 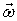 отличается от нуля в ограниченной области пространства.
отличается от нуля в ограниченной области пространства.
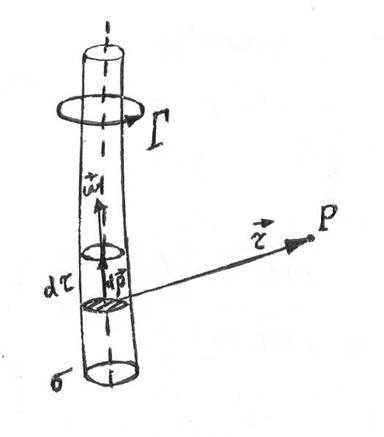
Рис. 2.3
Таким образом, задача сводится к отысканию векторной функции, являющейся решением векторного аналога уравнения Пуассона. Это решение можно записать в виде:

где 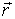 - радиус-вектор точки Р поля скоростей, в которой ведется наблюдение (рис. 2.3), следовательно,
- радиус-вектор точки Р поля скоростей, в которой ведется наблюдение (рис. 2.3), следовательно,
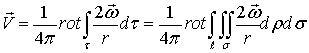
преобразуем:
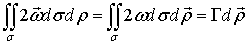
здесь: 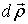 - малый участок элементарной вихревой нити, направление которого совпадает с
- малый участок элементарной вихревой нити, направление которого совпадает с 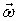 (рис. 2.3) .
(рис. 2.3) .
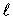 ,
,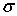 - длина и площадь сечения нити соответственно, следовательно
- длина и площадь сечения нити соответственно, следовательно

Операция 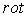 производится по координатам точки наблюдателя, поэтому
производится по координатам точки наблюдателя, поэтому 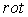 можно внести под знак интеграла:
можно внести под знак интеграла:

Воспользуемся формулой векторного анализа:
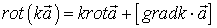
где 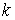 ,
,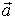 - произвольные скаляр и вектор, тогда
- произвольные скаляр и вектор, тогда
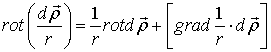
Поскольку  ;
;  , то формула для вычисления скорости приобретает вид гидродинамического аналога формулы Био-Савара теории электромагнетизма:
, то формула для вычисления скорости приобретает вид гидродинамического аналога формулы Био-Савара теории электромагнетизма:
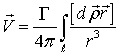
В качестве примера вычислим индуцированную скорость жидкости в центре вихревого кольца радиуса 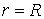 (рис. 2.4)
(рис. 2.4)
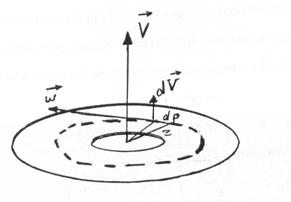
Рис. 2.4
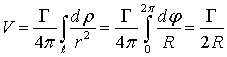
Вектор скорости направлен так, чтобы видеть с его конца вектор угловой скорости направленным против часовой стрелки. Согласно более подробному изучению движения вихревых колец [4] изолированное вихревое кольцо движется без изменения формы вдоль своей оси симметрии с примерно постоянной скоростью малой по сравнению со скоростью жидкости, находящейся в непосредственной близости с круговой осью; она может быть больше или меньше скорости жидкости в центре вихревого кольца, совпадает с ней по направлению и для ее вычисления можно использовать формулу
 ,
,
где  ,
,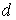 - диаметры большой и малой окружностей тороидального вихря.
- диаметры большой и малой окружностей тороидального вихря.
Пользуясь гидродинамическим аналогом закона Био-Савара можно получить общее представление о взаимодействии вихревых колец. В том случае, когда два вихревых кольца одного и того же направления вращения, движутся вдоль одной оси, их движение представляет собой нечто цельное, причем их действие друг на друга выражается в том, что скорость первого кольца уменьшается, а радиус увеличивается, тогда как радиус второго уменьшается, а скорость возрастает; второе кольцо нагоняет первое и при благоприятном соотношении между размерами и интенсивностью колец второе кольцо может догнать первое и пройти сквозь него. После этого кольца меняются ролями, и картина может повториться. Это явление называют игрой колец [4]. При движении двух одинаковых колец навстречу друг другу их размер возрастают, а поступательное движение замедляется, так как будто бы плоскость, расположенная посредине между ними, является для них непроницаемой. Точно также приближающееся к твердой плоской поверхности вихревое кольцо никогда ее не достигает, а, неограниченно увеличиваясь, расстилается по плоскости. Если кольцо встречает при своем движении нож, острый край которого перпендикулярен плоскости кольца, то оно, пройдя нож, восстанавливает свою форму.
Поверхность раздела двух потоков жидкости, имеющих различные скорости, можно рассматривать, как систему вихревых нитей, расположенных на поверхности раздела перпендикулярно линиям тока (рис. 2.5).

Рис. 2.5
Относительная скорость в средней части области раздела меньше, чем на периферии, поэтому давление в средней области больше, чем на периферии. Следовательно, жидкость будет перетекать от средней части к периферии, т.е. область раздела будет увеличиваться и поверхность контакта двух потоков, в конце концов, распадется на отдельные вихри, образуя квазипериодическую структуру [5].
С помощью гидродинамического аналога закона Био-Савара можно доказать теоремы, установленные Н.Е. Жуковским [6] для системы, состоящей из двух параллельных вихрей и для замкнутого вихревого кольца. Формулировку первой из них приведем в виде:
- два параллельных вихря одинакового напряжения, вращающихся в противоположные стороны, сообщают безграничной массе жидкости количество движения, отнесенное к единице длины вихря, равное произведению циркуляции вихрей на расстояние между их осями и плотность жидкости.
Формулировку второй можно дать в такой форме:
- замкнутый плоский вихревой шнур сообщает неограниченной массе жидкости, внутри которой он находится, количество движения равное произведению циркуляции вихря на его площадь и на плотность жидкости.
Эти теоремы позволили Н.Е. Жуковскому успешно решить задачи о взаимодействии потоков с окружающими жидкость твердыми телами, в частности, определить составляющие силы сопротивления движению тел в жидкости – лобовое сопротивление и подъемную силу.
С помощью первой теоремы Н.Е. Жуковский [6] решил задачу о лобовом сопротивлении цилиндрического тела, используя систему вихрей, которую принято называть дорожкой Кармана, а вторая позволила распространить решение на случай движения жидкости в трех измерениях.
Из первой теоремы следует [7], что:
1) один изолированный прямолинейный вихрь не может сообщить жидкости какого-либо количества движения,
2) потенциальное течение, т.е. невихревое движение жидкости, аналогично поступательному равномерному движению твердого тела вдоль прямой, может иметь место только при отсутствии сопротивления, требующего для преодоления потерь количества движения потока.
Кроме того, вторая теорема позволяет весьма просто вычислить силы давления неограниченного потока жидкости на пластины или отверстия произвольной формы. По теореме об изменении количества движения – сила динамического давления жидкости равна производной по времени от количества движения, поэтому с помощью второй теоремы имеем:
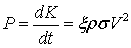
где 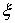 - коэффициент расхода жидкости при истечении ее через отверстие в тонкой стенке, а
- коэффициент расхода жидкости при истечении ее через отверстие в тонкой стенке, а 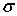 - площадь отверстия. Если высота уровня жидкости над отверстием -
- площадь отверстия. Если высота уровня жидкости над отверстием - 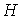 , то
, то 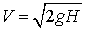 , а, следовательно,
, а, следовательно,
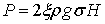
что находится в полном согласии с известным из гидравлики правилом: сила динамического давления истекающей из тонкого отверстия струи жидкости равна удвоенной силе статического давления на плоскость поперечного сечения струи.
Другая составляющая силы сопротивления – подъемная сила была определена Н.Е. Жуковским с помощью гипотезы о присоединенных вихрях [8], которая состоит в том, что твердое тело можно заменить системой вихрей, таких, что их действие сохраняет структуру окружающего тела потока, т.е. оставляет распределение скоростей в потоке таким же как и при обтекании твердого тела. Такая замена твердого тела – воображаемым, заполненным жидкостью, ограниченным замкнутой линией тока пространством – позволяет считать всю область односвязной, становится возможным применение теорем о вихрях, установленных для неограниченной жидкости. Отметим, что теорема Гельмгольца о движении вихрей не может быть распространена на вихри, введенные вместо твердого тела, поскольку их расположение подчиняется требованиям, вытекающим из условия, что они заменяют твердое тело. В остальном же эти вихри подчиняются теоремам Гельмгольца и в отличие от свободных вихрей их называют присоединенными вихрями.
Гипотеза о присоединенных вихрях совместно с постулатом Жуковского и Чаплыгина о конечной скорости на задней кромке обтекаемого жидкостью тела позволила Жуковскому установить теорему о подъемной силе [3]:
- величина подъемной силы плоскопараллельного потока, обтекающего тело неограниченной длины, отнесенная к единице его длины, равна произведению скорости набегающего потока, плотности жидкости и циркуляции скорости, а направление силы повернуто по отношению к набегающему потоку на 90° против циркуляции.
Гипотеза о замене твердого тела присоединенным вихрем не противоречит теоремам Жуковского о вихрях, т.к. на задней острой кромке тела сразу после начала движения образуется так называемый начальный вихрь, вместе с ним можно наблюдать развитие циркуляционного течения вокруг тела [9]. Если задняя кромка тела не является острой, то за телом возникает система вихрей.
Изложенный метод, состоящий в наложении течения с циркуляцией на потенциальное поле течения, можно использовать также и для решения задачи о движении жидкости вблизи вращающихся твердых тел или воздушных воронок, которые часто образуются вокруг отверстий в дне сосуда, через которые вытекает жидкость. Если в этом случае поток можно считать плоским, то в качестве потенциала скоростей можно принять

где 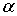 - центральный угол окружностей, которые являются линиями тока,
- центральный угол окружностей, которые являются линиями тока,
 - циркуляция потока.
- циркуляция потока.
Поверхности равного потенциала – плоскости проходящие через начало координат.
Скорость течения:
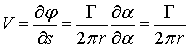
При 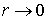 ,
, 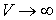 , поэтому реально такой поток может существовать только вне некоторой области конечного радиуса, а сама эта область вблизи оси вращения жидкости может быть заполнена твердым телом или состоять из жидкости, движение которой не является потенциальным, или состоять из другой более легкой жидкости (например, воздуха). Уравнение поверхности, например, образовавшийся в этом случае воздушной воронки, можно получить, применяя уравнение Бернулли к двум линиям тока:
, поэтому реально такой поток может существовать только вне некоторой области конечного радиуса, а сама эта область вблизи оси вращения жидкости может быть заполнена твердым телом или состоять из жидкости, движение которой не является потенциальным, или состоять из другой более легкой жидкости (например, воздуха). Уравнение поверхности, например, образовавшийся в этом случае воздушной воронки, можно получить, применяя уравнение Бернулли к двум линиям тока:
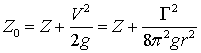
Изложенное указывает на важную роль вихревых образований в формировании течений жидкости и их взаимодействия с окружающей средой. Установленные в гл.1 принципы позволяют описать взаимодействие жидкости с твердыми телами, накладывая течения с циркуляцией на безвихревые течения, однако эти методы не могут быть распространены на описание механизмов появления и исчезновения вихрей, поэтому они нуждаются в дополнении и развитии.
§3. Поведение вихревых образований.
Исходные предпосылки общей теории вихрей, которой посвящена монография [10], не выходят за рамки принципов, изложенных в гл.1.
Обзор посвященных вихрям работ содержится также в [11], вместе с тем следует указать, что предложенный здесь вариант построения теории вихревых движений полагает в качестве одного из исходных пунктов уравнение состояния идеального газа, а, следовательно, результаты, полученные в этой работе, не могут претендовать на описание вихревых движений в жидкостях, тогда как закономерности в поведении вихрей носят общий для газов и жидкостей характер. Аналогичный упрек следует отнести и к работе [12].
В [14] предложена гипотеза, позволяющая описывать поведение вихрей в жидкости, которая может быть сформулирована в виде: сплошная среда, не содержащая разрывов, движется таким образом, что выполняется система уравнений:
 (2.3)
(2.3)
где  – изменение плотности в единицу времени в данной точке за счет внутренних источников (стоков) массы.
– изменение плотности в единицу времени в данной точке за счет внутренних источников (стоков) массы.
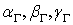 - коэффициенты пропорциональности, зависящие от циркуляции скорости
- коэффициенты пропорциональности, зависящие от циркуляции скорости  и состояния поверхности; в простейшем случае, например, коэффициент
и состояния поверхности; в простейшем случае, например, коэффициент 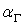 может быть равен
может быть равен 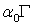 , где
, где  – константа, зависящая от качества поверхности.
– константа, зависящая от качества поверхности.
Если среда несжимаема, а источники (стоки) отсутствуют, то этой системе уравнений можно придать вид:
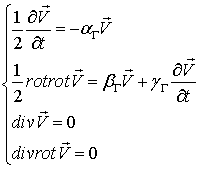 (2.4)
(2.4)
Эти уравнения можно записать в ином виде, если воспользоваться определением угловой скорости согласно (2.1). С этой целью возьмем от обеих частей первого уравнения системы (2.4) операцию rot, после чего эта система примет вид:
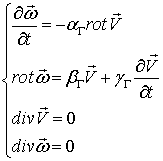 (2.5)
(2.5)
Выясним смысл этих уравнений. Последнее из них есть тождество векторного анализа. Третье уравнение представляет собой уравнение непрерывности, записанное для несжимаемой жидкости при отсутствии источников (стоков) масс. Решением первого уравнения системы (2.4) является
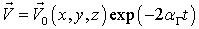
где 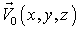 функция, описывающая поле скоростей жидкости в начальный момент времени.
функция, описывающая поле скоростей жидкости в начальный момент времени.
Отсюда следует, что первое уравнение системы (2.4) отражает замедление поступательного движения жидкости со временем.
Нетрудно видеть, что из первого уравнения системы (2.5) следует
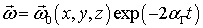
где  функция, определяющая поле угловых скоростей жидкости в начальный момент времени, то есть это уравнение описывает угасание вихревого движения в жидкости.
функция, определяющая поле угловых скоростей жидкости в начальный момент времени, то есть это уравнение описывает угасание вихревого движения в жидкости.
Таким образом, первые уравнения систем (2.3, 2.4, 2.5) описывают диссипацию энергии видимого движения жидкости.
Роль первого слагаемого в правой части второго уравнения систем (2.4, 2.5) становится понятной, если рассмотреть случай, когда 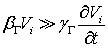 для всех i=1, 2, 3, тогда это уравнение примет вид:
для всех i=1, 2, 3, тогда это уравнение примет вид:
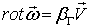
откуда следует, что в этом случае вектор вихря угловой скорости коаксиален вектору скорости жидкости, то есть имеет место ситуация, которая реализуется при тороидальном течении. Применяя к обеим частям последнего равенства операцию rot и воспользовавшись первым уравнением системы (2.5), получим:

- уравнение диффузии вихревых образований.
Если предыдущее равенство продифференцировать по времени и снова воспользоваться первым уравнением системы (2.5), то получим:

- уравнение диффузии для скорости частиц жидкости. Таким образом, первое слагаемое второго уравнения систем (2.3, 2.4, 2.5) отражает процессы диффузии вихревых образований и "быстрых" частиц жидкости от слоя к слою.
Роль второго слагаемого в правой части второго уравнения систем (2.4, 2.5) выясним, если рассмотрим случай, когда  для всех i=1,2,3, тогда это уравнение примет вид:
для всех i=1,2,3, тогда это уравнение примет вид:

Продифференцировав по времени левую и правую части этого уравнения и подставив вместо  его значение из первого уравнения системы (2.5), получим:
его значение из первого уравнения системы (2.5), получим:
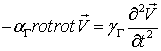
Воспользовавшись формулой векторного анализа:  &n и третьим уравнением системы (2.5), последнему уравнению можно придать вид:
&n и третьим уравнением системы (2.5), последнему уравнению можно придать вид:
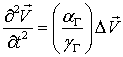
Аналогичное уравнение можно получить и для вектора угловой скорости жидкости - 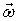 . Это уравнение описывает процесс распространения возникающих в жидкости возмущений, следовательно, второе слагаемое в правой части второго уравнения систем уравнений (2.3, 2.4, 2.5) отражает процесс передачи возмущений в жидкости от точки к точке.
. Это уравнение описывает процесс распространения возникающих в жидкости возмущений, следовательно, второе слагаемое в правой части второго уравнения систем уравнений (2.3, 2.4, 2.5) отражает процесс передачи возмущений в жидкости от точки к точке.
Обозначим 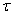 время, за которое происходит обмен путем диффузии между слоями жидкости с различными скоростями, находящимися на расстоянии порядка масштаба задачи -
время, за которое происходит обмен путем диффузии между слоями жидкости с различными скоростями, находящимися на расстоянии порядка масштаба задачи - 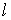 . Оценим это время. Опустив во втором уравнении системы (2.4) член
. Оценим это время. Опустив во втором уравнении системы (2.4) член  , получим:
, получим:
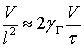
отсюда:
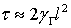
Для того, чтобы не создавалось перепадов скоростей между слоями жидкости, т.е. тангенциальных разрывов, которые, распадаясь, ведут к турбулизации потока, необходимо, чтобы время обмена между слоями на расстояниях порядка характерного масштаба задачи было на несколько порядков больше интервала времени, в течении которого возмущение проходит вместе с потоком со средней скоростью 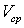 , расстояние
, расстояние 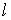 - порядка масштаба задачи:
- порядка масштаба задачи: 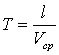 , т.е. успевает установиться плавный профиль скоростей. Исходя из этого, следует считать, что
, т.е. успевает установиться плавный профиль скоростей. Исходя из этого, следует считать, что
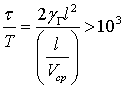
если положить:
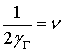 ,
,
где  - коэффициент кинематической вязкости, то получим:
- коэффициент кинематической вязкости, то получим:
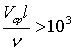
или число Рейнольдса Re > 103, что находится в соответствии с опытом Рейнольдса. Отметим, что отклонение коэффициента сопротивления от прямой Гагена-Пуазейля, начинается при числах Рейнольдса 1000-1100 [9].&p
Целесообразно опробовать предложенную выше систему уравнений в задачах о течениях вязкой жидкости, для которых хорошо известны решения, полученные на основе традиционных представлений, в частности, рассмотрим задачу Пуазейля об установившемся течении в трубе круглого сечения и задачу Стокса об обтекании шара потоком жидкости.
§4. Медленное течение вязкой жидкости в горизонтальной трубе круглого сечения.
Рассмотрим медленное течение жидкости внутри прямого кругового цилиндра, расположенного горизонтально. Воспользуемся цилиндрической системой координат (рис. 2.6)
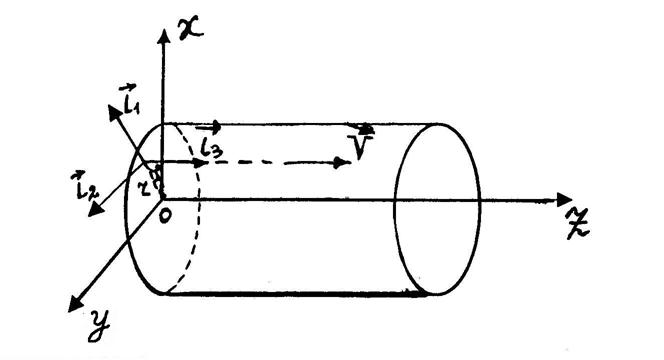
Рис. 2.6
Обозначим: 
Поскольку движение медленное, то в правой части второго уравнения системы (2.4) слагаемое 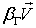 можно опустить и написать
можно опустить и написать

Заменяя с помощью этого соотношения первый член в левой части уравнения гидродинамики в напряжениях (1.9), получим:
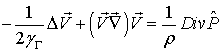
Инерционным членом в этом уравнении, поскольку рассматриваем медленные движения жидкости, можно пренебречь и придать ему вид:
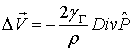
Учтем, что имеет место осевая симметрия, а, следовательно, входящие в это уравнение величины не зависят от угла 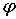 , и будем считать трубу бесконечно длинной, а течение установившимся, и потому скорость потока направленной вдоль оси трубы. В этом случае из трех компонент скорости отлична от нуля только одна
, и будем считать трубу бесконечно длинной, а течение установившимся, и потому скорость потока направленной вдоль оси трубы. В этом случае из трех компонент скорости отлична от нуля только одна 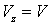 и последнее уравнение примет вид:
и последнее уравнение примет вид:
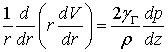
Левая часть этого уравнения может зависеть только от 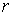 , а правая от
, а правая от 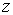 , поэтому равенство их возможно лишь в том случае, если каждая из них представляет собой постоянную величину. Обозначим
, поэтому равенство их возможно лишь в том случае, если каждая из них представляет собой постоянную величину. Обозначим 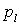 разность давлений на участке трубы длиной
разность давлений на участке трубы длиной 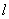 , тогда
, тогда

Таким образом, необходимо найти решение уравнения:
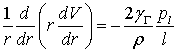
удовлетворяющее краевым условиям равенства нулю скорости потока на поверхности трубы и ее ограниченности на оси трубы. Таким решением является:

причем:
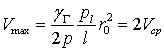
следовательно, секундный объемный расход жидкости равен:
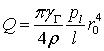
Это соотношение совпадает с законом Пуазейля: при достаточно медленном течении вязкой несжимаемой жидкости по цилиндрической трубе круглого сечения секундный объемный расход пропорционален перепаду давления, отнесенному к длине трубы, и четвертой степени ее радиуса.
§5. Обтекание шара медленным потоком жидкости.
Рассмотрим задачу Стокса о медленном обтекании шара стационарным потоком вязкой жидкости. С этой целью введем сферическую систему координат с центром, совпадающим с центром шара (рис. 2.7).
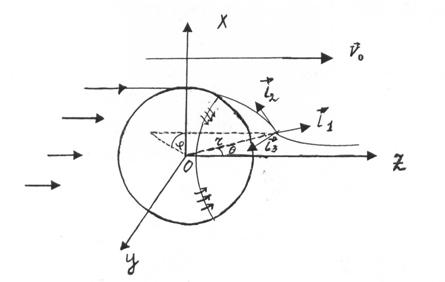
Рис. 2.7
Обозначим:
скорость потока:  ,
,
угловую скорость: 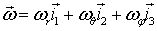 ,
,
скорость и давление набегающего потока: 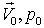 ,
,
радиус шара:  .
.
Воспользуемся вторым уравнением системы (2.5); взяв от обеих его частей операцию rot, получим:

С учетом первого уравнения этой системы отсюда:
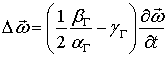
Будем считать угловую скорость независящей от времени, тогда последнее уравнение, примет вид:

Вихревые линии в этом случае представляют собой окружности, лежащие в плоскости перпендикулярной оси 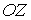 , поэтому
, поэтому 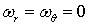 ,
,  , причем в силу осевой симметрии
, причем в силу осевой симметрии  зависит только от
зависит только от 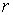 и
и  . Отсюда следует, что последнее уравнение, эквивалентно уравнению, имеющему вид:
. Отсюда следует, что последнее уравнение, эквивалентно уравнению, имеющему вид:
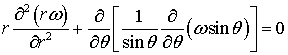
решение которого должно удовлетворять краевому условию:
 при
при 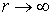 .
.
Нетрудно видеть, что таким решением будет:
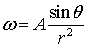
где 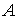 - постоянная величина.
- постоянная величина.
Для отыскания поля скоростей используем определение угловой скорости (2.1), которое в данном случае приводит к уравнению:

и уравнение неразрывности в виде:
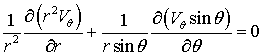
Решение системы, состоящей из этих уравнений, должно отвечать граничным условиям:

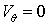 при
при 
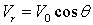
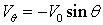 при
при 
Если положить  , то таким решением является:
, то таким решением является:


Для определения давления воспользуемся уравнением гидродинамики в напряжениях (1.9), причем будем считать движение жидкости медленным, если можно положить
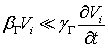
В этом случае из второго уравнения системы (2.5) следует

Подставив это соотношение в уравнение гидродинамики в напряжениях (1.9), записанное для случая отсутствия объемных сил, получим:
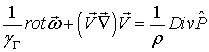
или с учетом (2.1) и полагая 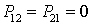 ,
, 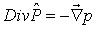 можно записать:
можно записать:
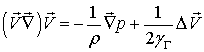
где  – давление, скалярная величина.
– давление, скалярная величина.
Второе слагаемое в правой части этого уравнения аналогично слагаемому, учитывающему в уравнении Навье-Стокса силы, обусловленные вязкостью жидкости. Если пренебречь инерционными слагаемыми, то из последнего уравнения следует:
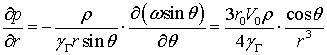
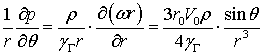
отсюда:
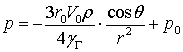
Поскольку последнее слагаемое в уравнении гидродинамики в напряжениях, записанное выше для данного случая, свидетельствует о наличии силы, аналогичной силам вязкости, то для касательной составляющей напряжения этой силы на поверхности шара можно записать:

Умножим полученное напряжение силы трения и давление на элементарную площадку в форме пояса, охватывающую шар - 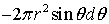 , после чего полученные элементарные силы спроектируем на направление скорости набегающего потока и проинтегрируем полученное выражение по поверхности шара (от 0 до
, после чего полученные элементарные силы спроектируем на направление скорости набегающего потока и проинтегрируем полученное выражение по поверхности шара (от 0 до 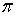 ). В результате получим проекцию силы сопротивления движению тела, приложенной к нему со стороны жидкости, на направление набегающего потока
). В результате получим проекцию силы сопротивления движению тела, приложенной к нему со стороны жидкости, на направление набегающего потока

Это выражение совпадает с формулой Стокса, если положить  , где
, где  коэффициент кинематической вязкости.
коэффициент кинематической вязкости.
Проведенное рассмотрение решения традиционных задач гидродинамики с помощью изложенной в §3 гипотезы о поведении вихревых образований свидетельствует с одной стороны в пользу ее справедливости, а с другой указывает на целесообразность более широкого ее использования.




![]()
![]()
![]() (2.1)
(2.1)

![]()
![]()
![]()
![]()
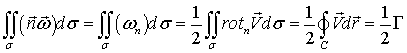 (2.2)
(2.2)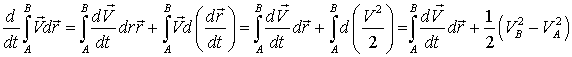

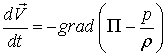
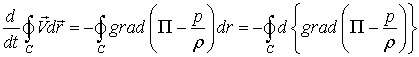
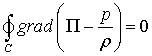
![]()
![]()
![]()
![]()

![]()
![]() для
для ![]()
![]()
![]() для
для ![]()
![]()
![]()
![]()
![]()
![]()
![]()


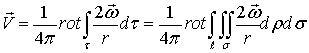
![]()


![]()
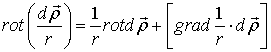
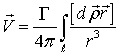

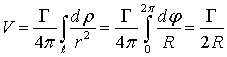
 ,
,
![]()
![]()
![]()
![]()
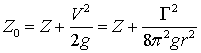
 (2.3)
(2.3)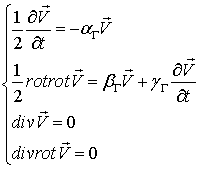 (2.4)
(2.4)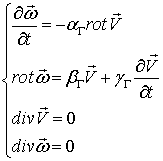 (2.5)
(2.5)![]()
![]()
![]()



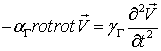
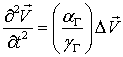
![]()
![]()
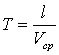 , т.е. успевает установиться плавный профиль скоростей. Исходя из этого, следует считать, что
, т.е. успевает установиться плавный профиль скоростей. Исходя из этого, следует считать, что
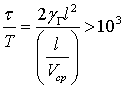
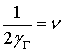 ,
,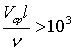


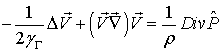
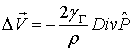
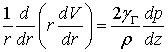
![]()
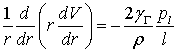

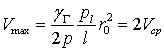
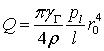

![]() ,
,![]() ,
,![]() ,
,![]() .
.![]()
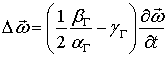
![]()
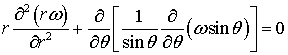
![]()

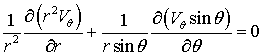


![]()

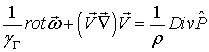
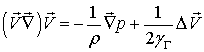
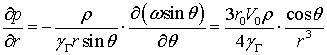
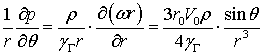
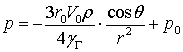


 , где
, где 
