ГЛАВА III.
Общее уравнение поля в задачах гидродинамики.
Изложенной в предыдущей главе гипотезе, отражающей коллективное взаимодействие отдельных частей системы между собой, можно придать более компактный вид.
§1. Общее уравнение поля.
Обратимся к рассмотрению в общем случае изложенной в предыдущей главе гипотезы, описывающей поведение вихрей. Из второго уравнения системы (2.5) с учетом (2.1) следует:

Если скорость невелика, так что можно положить  для всех
для всех  , то последнее уравнение преобразуется к виду:
, то последнее уравнение преобразуется к виду:

Заменив в уравнении гидродинамики в напряжениях с помощью этого соотношения частную производную по времени, найдем:

Если положить в этом уравнении:
 ,
,
где 
 - тензорная единица, а
- тензорная единица, а  - давление, скалярная величина, физический смысл которой совпадает с давлением, входящим в закон Паскаля гидростатики и законы термодинамики, то последнее уравнение принимает вид:
- давление, скалярная величина, физический смысл которой совпадает с давлением, входящим в закон Паскаля гидростатики и законы термодинамики, то последнее уравнение принимает вид:

Это уравнение совпадает со стационарным уравнением Навье-Стокса, если положить 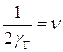 , где
, где  - коэффициент кинематической вязкости.
- коэффициент кинематической вязкости.
Отсюда следует, что с помощью системы уравнений (2.5) или эквивалентной ей системы (2.4) можно получить не только решения задач, приведенных в предыдущей главе, но также и другие известные решения стационарного уравнения Навье-Стокса.
Системы уравнений (2.4; 2.5) можно свести к уравнением в частных производных второго порядка относительно  или
или  . В частности, если второе уравнение системы (2.4) продифференцировать по времени, то можно написать:
. В частности, если второе уравнение системы (2.4) продифференцировать по времени, то можно написать:

и, заменяя производную по времени от скорости в левой части этого уравнения ее значением из первого уравнения той же системы, получим:
 (3 1)
(3 1)
Если второе уравнение системы (2.5) продифференцировать по времени, а затем взять от обеих частей вновь полученного уравнения операцию  , то оно примет вид:
, то оно примет вид:
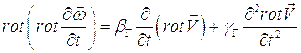
Заменив  его значением:
его значением:  из первого уравнения этой системы и воспользовавшись (2.1) будем иметь:
из первого уравнения этой системы и воспользовавшись (2.1) будем иметь:
 (3.2)
(3.2)
Очевидно, что все операции дифференцирования проведены в предположении, что коэффициенты  не зависят явно от времени и координат. Отметим важный результат, состоящий в том, что дифференциальные уравнения для определения
не зависят явно от времени и координат. Отметим важный результат, состоящий в том, что дифференциальные уравнения для определения  и
и  имеют идентичный вид.
имеют идентичный вид.
Можно ввести векторный и скалярный потенциалы -  и
и  , такие что:
, такие что:


причем:  , тогда системы уравнений (2.4, 2.5) сводятся к следующей:
, тогда системы уравнений (2.4, 2.5) сводятся к следующей:
 (3.3)
(3.3)
Нетрудно видеть, что эти уравнения идентичны уравнениям (3.1, 3.2). Этот результат дает основания полагать, что для описания течения жидкости достаточно одной функции. Ведем  - вектор такой, что справедливо уравнение
- вектор такой, что справедливо уравнение
 ; (3.4)
; (3.4)
В таком случае соотношения (3.1 - 3.4) выполняются, если положить:





Таким образом, можно констатировать, что уравнение
 (3.5)
(3.5)
где: ,
,  , позволяет вычислить характеристики гидромеханического поля -
, позволяет вычислить характеристики гидромеханического поля -  . Отметим также, что если последним слагаемым в левой части этого уравнения можно пренебречь, то оно приобретает вид волнового уравнения, причем, если в этом случае под
. Отметим также, что если последним слагаемым в левой части этого уравнения можно пренебречь, то оно приобретает вид волнового уравнения, причем, если в этом случае под  понимать сжатие среды, а под
понимать сжатие среды, а под  - скорость распространения возмущений, то оно позволяет описывать распространение звуковых колебаний.
- скорость распространения возмущений, то оно позволяет описывать распространение звуковых колебаний.
В том случае, когда можно пренебречь вторым членом в уравнении (3.5), оно становится идентичным уравнению диффузии, если под  подразумевать концентрацию, а под
подразумевать концентрацию, а под  - коэффициент диффузии, или уравнению теплопроводности, если под
- коэффициент диффузии, или уравнению теплопроводности, если под  подразумевать температуру, а под
подразумевать температуру, а под  - коэффициент температуропроводности. Нетрудно видеть, что соотношения, описывающие стационарные гравитационное и электрическое поля удовлетворяют уравнению (3.5). Отмеченные обстоятельства и послужили основанием для того, чтобы в работе [14] назвать уравнение (3.5) общим уравнением поля. Обратим внимание на то, что, будучи записанным для скорости, общее уравнение поля отчетливо демонстрирует отличие скорости движения среды от скорости распространения возмущений в среде.
- коэффициент температуропроводности. Нетрудно видеть, что соотношения, описывающие стационарные гравитационное и электрическое поля удовлетворяют уравнению (3.5). Отмеченные обстоятельства и послужили основанием для того, чтобы в работе [14] назвать уравнение (3.5) общим уравнением поля. Обратим внимание на то, что, будучи записанным для скорости, общее уравнение поля отчетливо демонстрирует отличие скорости движения среды от скорости распространения возмущений в среде.
Исходя из изложенного, следует считать целесообразным использование при решении задач гидродинамики системы уравнений
 (3.6)
(3.6)
где
 - дивергенция тензора напряжений,
- дивергенция тензора напряжений,
 - поле объемных сил,
- поле объемных сил,
 - плотность среды,
- плотность среды,
 - скорость течения жидкости,
- скорость течения жидкости,

Обычно вместо второго уравнения системы (3.6) используют уравнение неразрывности среды, однако, как отмечалось в первой главе, в этом случае система уравнений является незамкнутой. Система уравнений (3.6) свободна от этого недостатка, вместе с тем уравнение неразрывности среды использовалось при выводе общего уравнения поля в качестве одного из исходных положений. В том случае, когда можно положить  для всех
для всех  , второе уравнение системы (2.11) переходит в уравнение Лапласа, а первое - в стационарное уравнение Эйлера, то есть эта система уравнений описывает потенциальные течения. Если в качестве отправной точки при решении задач гидромеханики использовать систему уравнений (3.6), то следует признать, что нестационарные течения в целом не могут быть потенциальными; потенциальными могут считаться в течение некоторого интервала времени лишь отдельные участки нестационарных течений.
, второе уравнение системы (2.11) переходит в уравнение Лапласа, а первое - в стационарное уравнение Эйлера, то есть эта система уравнений описывает потенциальные течения. Если в качестве отправной точки при решении задач гидромеханики использовать систему уравнений (3.6), то следует признать, что нестационарные течения в целом не могут быть потенциальными; потенциальными могут считаться в течение некоторого интервала времени лишь отдельные участки нестационарных течений.
Стационарные уравнения Навье-Стокса можно также считать следствием системы уравнений (3.6). В самом деле, нетрудно видеть, что из первого уравнения системы (2.4) следует:

если условия задачи позволяют пренебречь последним слагаемым во втором уравнении системы (3.6), то этому уравнению можно придать вид:

следовательно, первое уравнение системы (3.6) принимает вид:

который идентичен уравнению Навье-Стокса, если положить  , где
, где  - коэффициент кинематической вязкости. Таким образом, стационарные уравнения Навье-Стокса можно рассматривать, как следствие системы уравнений (3.6).
- коэффициент кинематической вязкости. Таким образом, стационарные уравнения Навье-Стокса можно рассматривать, как следствие системы уравнений (3.6).
В том случае, когда для описания течения жидкости может быть использована декартова прямоугольная система координат, общее уравнение поля сводится к системе дифференциальных уравнений с разделяющимися переменными, что позволяет воспользоваться для отыскания решения стандартными методами. Покажем это на примере отрывного течения, возникающего при обтекании прямоугольного канала потоком жидкости перпендикулярным его оси.
§2. Расчет течения жидкости в прямоугольном канале, обтекаемом стационарным перпендикулярным его оси потоком.
Воспользуемся общим уравнением поля для определения поля скоростей жидкости в прямоугольном канале*), внешнюю границу которого обтекает поток жидкости со скоростью  , перпендикулярной его оси.
, перпендикулярной его оси.
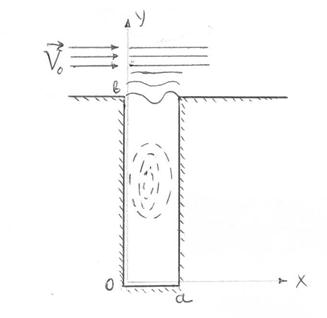
Рис. 3.1
Расположим декартову систему координат так, как это показано на рис.3.1. и введем безразмерные координаты, время и скорость, согласно:

здесь  - безразмерные координаты, время и скорость, а
- безразмерные координаты, время и скорость, а  - координаты, время и скорость в общепринятых единицах,
- координаты, время и скорость в общепринятых единицах,  - ширина и глубина канала, соответственно,
- ширина и глубина канала, соответственно,  - модуль скорости невозмущенной части обтекающего канал потока.
- модуль скорости невозмущенной части обтекающего канал потока.
Общее уравнение поля, записанное для скорости жидкости (второе уравнение системы (3.6)), примет вид:
 (3.7)
(3.7)
где: 
Далее, с целью упрощения, опустим значок  , однако будем помнить, что использующиеся в этом параграфе координаты, время и скорость - безразмерные величины. Начальные условия запишем в виде:
, однако будем помнить, что использующиеся в этом параграфе координаты, время и скорость - безразмерные величины. Начальные условия запишем в виде:
а) б)
 (3.8)
(3.8)
Скорость жидкости на границе раздела (вне канала и внутри него) терпит тангенциальный разрыв, который является неустойчивым образованием. Его поверхность, как показано в главе II §2, распадаясь, превращается в квазипериодическую систему вихрей. Поэтому граничные условия можно представить в виде:
а) б)


 (3.9)
(3.9)
На функции  ограничений не накладываем. Поскольку вблизи верхней границы канала имеют место квазипериодические изменения скорости, то будем считать, что функции
ограничений не накладываем. Поскольку вблизи верхней границы канала имеют место квазипериодические изменения скорости, то будем считать, что функции  и
и  можно разложить в ряды Фурье вида:
можно разложить в ряды Фурье вида:


Решение уравнения (3.6) ищем в виде:

где:  - общее решение этого уравнения с нулевыми граничными условиями и начальными условиями в форме (3.8)
- общее решение этого уравнения с нулевыми граничными условиями и начальными условиями в форме (3.8)
 - частное решение с нулевыми начальными условиями, удовлетворяющее граничным условиям в форме (3.9)
- частное решение с нулевыми начальными условиями, удовлетворяющее граничным условиям в форме (3.9)
Воспользовавшись теорией дифференциальных уравнений в частных производных второго порядка можно найти:



 ,
, 
Аналогичные соотношения справедливы для  , где вместо функций
, где вместо функций  следует поставить
следует поставить  .Из приведенных соотношений видно, что, при достаточно больших
.Из приведенных соотношений видно, что, при достаточно больших  , величина
, величина  близка к нулю, т.е., в конце концов, установится течение, которое не зависит от начальных условий:
близка к нулю, т.е., в конце концов, установится течение, которое не зависит от начальных условий:  .
.
Отметим, что функция  должна подчиняться уравнению:
должна подчиняться уравнению:

следовательно, компонента  удовлетворяет уравнению:
удовлетворяет уравнению:
 (3.10)
(3.10)
и граничным условиям:

причем 
На функцию  условия задачи ограничений не накладывают, а из условия
условия задачи ограничений не накладывают, а из условия  вытекает, что
вытекает, что  , следовательно
, следовательно  , где .
, где .
Решение уравнения (3.10) ищем в виде:

 (3.11)
(3.11)
причем:

После дифференцирования получим:




Подставляя эти соотношения в уравнение (З.10), убеждаемся, что (3.11) будет его решением, если:

или:

для всех 
Положим:

тогда:

Подставляя эти соотношения в последнее уравнение, убеждаемся, что оно удовлетворяется, если:

отсюда:


Из последнего уравнения:

Поскольку  - действительное число, то знак минус перед квадратным корнем следует опустить, поэтому:
- действительное число, то знак минус перед квадратным корнем следует опустить, поэтому:

следовательно:

Условие:  выполняется, если положить
выполняется, если положить  и
и  , где
, где 
Последнее из этих равенств эквивалентно уравнению:

или:

Следовательно, на границе между жидкостью в канале и обтекающем канал потоком реализуются только те пульсации, частоты которых отвечают условию:
 (3.12)
(3.12)
Отметим, что это явление напоминает квантование энергии в атомных системах.
Таким образом, решением уравнения (3.10) будет:
 (3.13)
(3.13)
где:



При:


Согласно граничному условию (3.9) при  :
:
 ,
,
причем  .
.
Следовательно, на границе между жидкостью, находящейся в канале и в обтекающем его потоке, возникают пульсации с частотами, отвечающими условию (3.12), причем:

Перейдем к определению компоненты  , которая отвечает уравнению:
, которая отвечает уравнению:
 (3.14)
(3.14)
и граничным условиям:

причем  .
.
На функции  и
и  условия задачи ограничений не накладывают.
условия задачи ограничений не накладывают.
Решение уравнения (3.13) ищем в виде:

причем: 




Подставив эти выражения в (3.14) получим, что это уравнение выполняется, если справедливо:

Положим:


где  ,
,  - постоянная величина, тогда из последнего уравнения следует:
- постоянная величина, тогда из последнего уравнения следует:

Эта система уравнений эквивалентна следующей:

отсюда:

Поскольку  - действительное число, то:
- действительное число, то:

следовательно:


Граничное условие  удовлетворяется автоматически, а из второго
удовлетворяется автоматически, а из второго
 следует:
следует:

Это означает, что:

Поскольку  а следовательно и
а следовательно и  , зависят от
, зависят от  и
и  , то от них зависит и функция
, то от них зависит и функция  .Отметим, что:
.Отметим, что:

или, с учетом полученных выше соотношений:


Поскольку  , то
, то
 (3.15)
(3.15)
Отметим, что:

Решением уравнения (3.14) будет:

При  , отсюда следует:
, отсюда следует:

Согласно граничным условиям (3.14):

Следовательно, для функции  справедливо:
справедливо:

Этот результат подтверждает сделанный ранее вывод, состоящий в том, что на границе канала возникают пульсации, имеющие дискретный спектр.
Отметим, что при  ,
,  ,
,  , тогда:
, тогда:

В этом случае компоненту  можно придать вид аналогичный
можно придать вид аналогичный  (3.13):
(3.13):

При
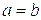 ,
,  ,
,  ,
,  ;
;

Если при этом  несильно зависит от
несильно зависит от  , то в первом приближении вклад гармоник, сдвиг по фазе между которыми
, то в первом приближении вклад гармоник, сдвиг по фазе между которыми  , может компенсироваться, тогда их сдвиг по фазе относительно
, может компенсироваться, тогда их сдвиг по фазе относительно  не будет зависеть от
не будет зависеть от 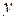 . Аналогичная ситуация может иметь место и для
. Аналогичная ситуация может иметь место и для  . Вместе с тем для отдельных гармоник, входящих в
. Вместе с тем для отдельных гармоник, входящих в  и
и  , сдвиг фаз может составлять
, сдвиг фаз может составлять  , то есть
, то есть


Если при этом  , то
, то  , то есть соотношение между компонентами скорости будет отвечать движению по окружности. Такая ситуация повторяется дважды, если
, то есть соотношение между компонентами скорости будет отвечать движению по окружности. Такая ситуация повторяется дважды, если  , тогда
, тогда  . Эта картина находится в согласии с экспериментальными данными о течении жидкости в канале при обтекании его потоком перпендикулярным оси [17].
. Эта картина находится в согласии с экспериментальными данными о течении жидкости в канале при обтекании его потоком перпендикулярным оси [17].
В результате проведенного рассмотрения можно утверждать, что по истечении достаточно большого промежутка времени в канале установится течение, скорость которого:
 (3.16)
(3.16)
причем:


где:
 ,
,
 ,
,



 - коэффициенты, получающиеся при разложении краевых функций
- коэффициенты, получающиеся при разложении краевых функций  в ряды Фурье.
в ряды Фурье.
 - амплитуды отдельных гармоник с частотами
- амплитуды отдельных гармоник с частотами  , из которых складываются пульсации на границе обтекаемого канала.
, из которых складываются пульсации на границе обтекаемого канала.
Исходя из изложенного при обтекании потоком жидкости прямоугольной каверны, ее следует рассматривать как источник возмущений, причем пульсации будут переносить энергию пропорциональную квадрату скорости

Из этой формулы следует, что энергетический спектр пульсаций скорости является дискретным, причем значения частот вычисляются по правилам, напоминающим правила квантования электромагнитной энергии. Кроме того, отметим, что поскольку распределение скоростей найдено, то, воспользовавшись приемом, аналогичным изложенному в главе II, §4, можно найти с помощью первого уравнения системы (3.6) и распределение давления в жидкости.
§3. Обтекание цилиндра однородным потоком жидкости.
Используем общее уравнение поля для определения поля скоростей за прямым круговым цилиндром бесконечной длины при обтекании перпендикулярным его образующей стационарным однородным потоком жидкости*). Поскольку течение можно считать плоским, то для описания поведения жидкости воспользуемся полярной системой отсчета (рис. 3.2.), причем под полярным радиусом будем понимать безразмерную величину  , где
, где  - величина отрезка от полюса до заданной точки, а
- величина отрезка от полюса до заданной точки, а  - радиус цилиндра.
- радиус цилиндра.
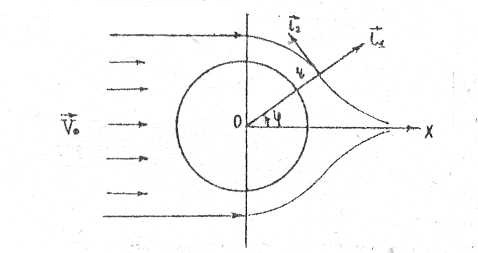
Рис. 3.2
Скорость потока:

здесь: - отношение вектора скорости потока в данной точке к модулю
- отношение вектора скорости потока в данной точке к модулю
скорости набегающего потока  .
.
Для описания течения используем общее уравнение поля в виде:
 (3.17)
(3.17)
где: 

 - лапласиан, взятый от вектора скорости.
- лапласиан, взятый от вектора скорости.

 - безразмерное время,
- безразмерное время,  - время в общепринятых единицах,
- время в общепринятых единицах,

Воспользовавшись выражением для лапласиана в полярных координатах, запишем вместо уравнения для вектора скорости (3.17) систему уравнений для проекций скорости на оси полярной системы координат.
 (3.18)
(3.18)
Начальные условия для компонентов скорости:




граничные условия:



на функцию  - ограничений не накладывается.
- ограничений не накладывается.
Если ввести функции:
 (3.19)
(3.19)
то эта система уравнений сводится к системе уравнений с разделяющимися переменными:
 (3.20)
(3.20)
Отметим, что

тривиальное решение первого из уравнений системы (3.20). Функцию  будем искать в виде суммы:
будем искать в виде суммы:
 ,
,
где  - общее решение уравнения (3.20) с заданными начальными условиями и нулевыми граничными условиями
- общее решение уравнения (3.20) с заданными начальными условиями и нулевыми граничными условиями
 - частное решение уравнения (3.20), отвечающее заданным граничным и нулевым начальным условиям.
- частное решение уравнения (3.20), отвечающее заданным граничным и нулевым начальным условиям.
Общее решение  ищем в виде:
ищем в виде:


Подставим в исходное уравнение, получим:

где  - постоянная величина, отсюда:
- постоянная величина, отсюда:

Решением этого уравнения будет:

где  и
и  - константы, значения которых подбираются так, чтобы удовлетворялись начальные условия.
- константы, значения которых подбираются так, чтобы удовлетворялись начальные условия.
Отметим, что при достаточно больших  значения функции
значения функции  , а значит и функции
, а значит и функции  станут весьма малыми, следовательно, при
станут весьма малыми, следовательно, при  :
:  .
.
Частное решение  , ищем в виде:
, ищем в виде:

Подставив это выражение в (3.20), получим:

откуда:
 ,
,
где  -действительное положительное число.
-действительное положительное число.
Это соотношение эквивалентно уравнениям:
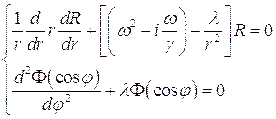 (3.21)
(3.21)
Если положить  , то
, то

и второе из уравнений (3.21) примет вид:

Это уравнение близко по форме уравнению Лежандра, поэтому его решение будем искать в форме полинома:

Подставляя это выражение в последнее уравнение, получим:
 ,
,
следовательно,  будет решением, если:
будет решением, если:

При  совокупность полиномов:
совокупность полиномов:

будет являться искомым решением.
Первое из уравнений (3.21), положив
 и
и  ,
,
преобразуем к виду:

Решением этого уравнения является функция:

где  функции Ханкеля первого и второго рода порядка
функции Ханкеля первого и второго рода порядка  .
.
Таким образом, частным решением уравнения (3.20) будет:
 (3.22)
(3.22)
Выражения для компонент скорости будем искать в виде:

Подставим эти выражения в уравнение (3.18) с учетом (3.19) и (3.22), получим:

 здесь
здесь  , причем
, причем  , следовательно:
, следовательно:


Компоненты скорости должны отвечать краевому условию ограниченности на бесконечности, а, поскольку  неограниченно возрастает при
неограниченно возрастает при  , то слагаемые, содержащие
, то слагаемые, содержащие  следует опустить.
следует опустить.
Из краевого условия  следует, что
следует, что  , где
, где  - корень уравнения
- корень уравнения  ,
,  то есть реализуются не любые значения частоты, а лишь отвечающие условию
то есть реализуются не любые значения частоты, а лишь отвечающие условию  , что эквивалентно:
, что эквивалентно:

откуда:
 (3.23)
(3.23)
где  - модуль
- модуль  -того корня функции Ханкеля первого рода
-того корня функции Ханкеля первого рода  -того порядка. Отметим, что частоты пульсаций компонент скорости, как и в случае обтекания прямоугольного углубления, образуют дискретный спектр, причем при
-того порядка. Отметим, что частоты пульсаций компонент скорости, как и в случае обтекания прямоугольного углубления, образуют дискретный спектр, причем при 

Краевые условия  ,
,  выполняются, если положить в полиноме
выполняются, если положить в полиноме  коэффициенты
коэффициенты  ,
,  , последующие определять по рекуррентному соотношению:
, последующие определять по рекуррентному соотношению:

 ;
; 
Таким образом, окончательно для компонент скорости будем иметь:
 (3.24)
(3.24)

Если условия таковы, что в первом приближении можно положить
 (3.25)
(3.25)
где  ,
,  подобраны так, чтобы выполнялось написанное равенство, а
подобраны так, чтобы выполнялось написанное равенство, а 
может и не совпадать с  , тогда
, тогда

Предположим, что в данных условиях доминирующую роль в этой сумме играет  -ое слагаемое, в этом случае
-ое слагаемое, в этом случае
 (3.26)
(3.26)
Согласно [19] для  -того корня функции Ханкеля
-того корня функции Ханкеля  -того порядка справедливо
-того порядка справедливо

где  - небольшая поправка, поэтому на основании равенства (3.26) можно утверждать, что радиальная компонента скорости
- небольшая поправка, поэтому на основании равенства (3.26) можно утверждать, что радиальная компонента скорости  должна обращаться в нуль при
должна обращаться в нуль при
 (3.27)
(3.27)
где  , причем
, причем  ,
, 
В этом случае радиальная составляющая скорости будет равна нулю, если  и далее с интервалом
и далее с интервалом  . Отметим, что для справедливости этого утверждения достаточно, чтобы соотношение (3.26) выполнялось вблизи корней функции
. Отметим, что для справедливости этого утверждения достаточно, чтобы соотношение (3.26) выполнялось вблизи корней функции 
Равенства (3.24) были получены исходя из того, что на величину нормальной к радиусу компоненты скорости на поверхности цилиндра ограничений не накладывается. Однако следует отметить, что реально имеет место "прилипание", т.е. обращение в нуль нормальной к радиусу компоненты скорости частиц жидкости на поверхности цилиндра. Такие частицы, из областей расположенных вблизи  , будут сноситься внешним потоком и медленно перемещаться вдоль плоскостей, параллельных внешнему потоку и отстоящих от плоскости симметрии на расстояниях
, будут сноситься внешним потоком и медленно перемещаться вдоль плоскостей, параллельных внешнему потоку и отстоящих от плоскости симметрии на расстояниях  . Вдоль линии пересечения этих плоскостей с плоскостями направленными вдоль радиусов, скорости жидкости будут равны нулю, если расстояние линий пересечения от оси цилиндра будут отвечать условно (3.27), т.е. вокруг линий, отвечающих этому условию, образуется цепочка вихревых шнуров. Вместе с тем следует иметь ввиду, что практически реализуются только те вихри у которых скорость на внешней стороне совпадает по направлению со скоростью внешнего потока, т.е. на практике будет иметь место только каждый второй, из отвечающих указанному условию вихревых шнуров, а следовательно расстояние между осями вихрей в цепочке по одну сторону от плоскости симметрии составит:
. Вдоль линии пересечения этих плоскостей с плоскостями направленными вдоль радиусов, скорости жидкости будут равны нулю, если расстояние линий пересечения от оси цилиндра будут отвечать условно (3.27), т.е. вокруг линий, отвечающих этому условию, образуется цепочка вихревых шнуров. Вместе с тем следует иметь ввиду, что практически реализуются только те вихри у которых скорость на внешней стороне совпадает по направлению со скоростью внешнего потока, т.е. на практике будет иметь место только каждый второй, из отвечающих указанному условию вихревых шнуров, а следовательно расстояние между осями вихрей в цепочке по одну сторону от плоскости симметрии составит:

Положение осей вихревых шнуров, находящихся на противоположной стороне плоскости симметрии будет сдвинуто по отношению к осям первого ряда на величину  , поскольку в формулу (3.24) для
, поскольку в формулу (3.24) для  входит функция
входит функция  , которая является нечетной и ее значения при замене
, которая является нечетной и ее значения при замене  на
на  сдвигаются вдоль оси
сдвигаются вдоль оси  на
на  . Таким образом за цилиндром образуется система вихревых цепочек (рис. 3.3), состоящая из сдвинутых друг относительно друга на величину
. Таким образом за цилиндром образуется система вихревых цепочек (рис. 3.3), состоящая из сдвинутых друг относительно друга на величину  рядов вихревых шнуров, расстояния между осями которых
рядов вихревых шнуров, расстояния между осями которых  ,а между рядами
,а между рядами 
Если предположить, что потоком увлекаются частицы жидкости с поверхности цилиндра вплоть до  , то
, то

Эта величина хорошо согласуется с вычислениями Кармана [17]: 0,281.
Рис 3.3
Если воспользоваться данными Жуковского [3] и положить границу невозмущенного потока на высоте  , то получим:
, то получим:

Эта величина находится в согласии со значением  , приведенным в [3].
, приведенным в [3].
Согласно [3,9] величина любого сопротивления тела, обтекаемого жидкостью, пропорциональна отношению  , вместе с тем, из изложенного следует, что это отношение тем меньше, чем ниже по течению удерживаются на поверхности тела "прилипшие" частицы, а это в свою очередь означает, что с целью уменьшения коэффициента лобового сопротивления профиль обтекаемого тела целесообразно делать таким, чтобы угол между касательной к поверхности тела и направлением внешнего потока был минимальным.
, вместе с тем, из изложенного следует, что это отношение тем меньше, чем ниже по течению удерживаются на поверхности тела "прилипшие" частицы, а это в свою очередь означает, что с целью уменьшения коэффициента лобового сопротивления профиль обтекаемого тела целесообразно делать таким, чтобы угол между касательной к поверхности тела и направлением внешнего потока был минимальным.
§4. Шар в однородном потоке жидкости.
Воспользуемся общим уравнением поля в виде (3.17) для решения задачи об обтекании шара однородным потоком жидкости*). Введем сферическую систему координат (рис. 3.4.), причем под скоростью, временем и радиусом будем понимать безразмерные величины, аналогичные введенным в предыдущем параграфе.
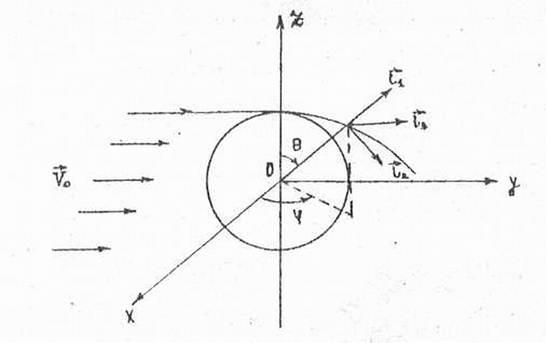

Рис 3.4
В этом случае векторное уравнение (3.17) эквивалентно трем скалярным:
 (3.28)
(3.28)

Учитывая, что  , то есть
, то есть
 (3.29)
(3.29)
и, обозначив



придадим системе уравнений (3.28) вид:
 (3.30)
(3.30)
Подставив в первое из этих уравнений полученное с помощью (3.29) выражение:
 (3.31)
(3.31)
получим

Обозначив

последнему уравнению можно придать вид:

Второе уравнение системы (3.30) запишем в виде:

Положив

получим

Для определения  , можно воспользоваться уравнением (3.31). Таким образом, исходная система уравнений (3.28) эквивалентна следующей системе:
, можно воспользоваться уравнением (3.31). Таким образом, исходная система уравнений (3.28) эквивалентна следующей системе:
 (3.32)
(3.32)
причем:
 ;
; 
Аналогично предыдущему можно представить решение этих уравнений в виде общего решения, удовлетворяющего заданным начальным и нулевым граничным условиям, и частного решения удовлетворяющего граничным условиям данной задачи:
При  ,
,  ; на
; на  - ограничения не накладываются
- ограничения не накладываются
Если  , то, при
, то, при 
 ,
,  ,
, 
При 



Частное решение первого из уравнений (3.32) ищем в виде:

Подставляя его в это уравнение получим:

откуда:
 (3.33)
(3.33)
где  - положительное число.
- положительное число.
Нетрудно видеть, что функция  должна удовлетворять уравнению
должна удовлетворять уравнению

и отвечать условиям однозначности и ограниченности в каждой точке сферы, то есть:

 ,
,
Если положить, что  можно представить в виде:
можно представить в виде:

то на основании последнего уравнения можно написать:

где  - положительное число.
- положительное число.
Следовательно, функция  должна удовлетворять уравнению:
должна удовлетворять уравнению:

и условию периодичности 
Отсюда следует, что  и линейно независимыми решениями этого уравнения являются:
и линейно независимыми решениями этого уравнения являются:  и
и  , причем
, причем  - целое число.
- целое число.
Функция  должна удовлетворять уравнению:
должна удовлетворять уравнению:

которое, путем введения новой переменной  , преобразуется к уравнению присоединенных функций
, преобразуется к уравнению присоединенных функций

причем:
 ,
, 
Если положить  , то решением этого уравнения будут присоединенные функции:
, то решением этого уравнения будут присоединенные функции:

где  - полином Лежандра степени
- полином Лежандра степени  ,
,  .
.
Для функции  на основании соотношения (3.33) получим:
на основании соотношения (3.33) получим:

полагая,  , преобразуем это уравнение к виду:
, преобразуем это уравнение к виду:

Решение ищем в виде ряда:

Он будет решением полученного уравнения, если выполняются условия:



…..

…
Если считать, что  , то для выполнения первого из этих условий необходимо:
, то для выполнения первого из этих условий необходимо:

отсюда следует, что  , либо
, либо  .
.
Тогда для выполнения второго условия необходимо положить:  , а последнее из этих уравнений дает рекуррентную формулу для определения
, а последнее из этих уравнений дает рекуррентную формулу для определения  по известному
по известному 


Для случая  эта формула приобретает вид:
эта формула приобретает вид:

или, полагая  , где
, где 

Для случая  будем иметь:
будем иметь:

или, полагая 

Последовательное применение этих формул дает:
для 

для 

Таким образом, решение дифференциального уравнения может быть представлено в виде:

где  и
и  произвольные константы, могут быть выбраны в соответствие с условиями задачи
произвольные константы, могут быть выбраны в соответствие с условиями задачи


Сходимость рядов  и
и  очевидна. Оставляя за рамками этой книги доказательства ортогональности, полноты и замкнутости функций
очевидна. Оставляя за рамками этой книги доказательства ортогональности, полноты и замкнутости функций  и
и  , отметим, что их построение, а следовательно и поведение при
, отметим, что их построение, а следовательно и поведение при  , аналогично функциям Ханкеля первого и второго рода. Если из двух значений
, аналогично функциям Ханкеля первого и второго рода. Если из двух значений

выбрать  со знаком "+", то условию ограниченности будет отвечать случай
со знаком "+", то условию ограниченности будет отвечать случай  , если взять
, если взять  со знаком "-", то
со знаком "-", то  . Для определенности выберем знак "-", тогда для функции
. Для определенности выберем знак "-", тогда для функции  справедливо:
справедливо:

Очевидно, что краевые условия  ;
;  будут выполняться, а условие
будут выполняться, а условие  выполняется, если
выполняется, если
 , т.е.
, т.е.  , где
, где  - к-ый корень уравнения
- к-ый корень уравнения  , отсюда
, отсюда

следовательно, реализуются не все частоты, а лишь  отвечающие этому условию. Отметим, что из этого условия следует соотношение аналогичные (3.23).
отвечающие этому условию. Отметим, что из этого условия следует соотношение аналогичные (3.23).
Таким образом, для радиальной составляющей скорости можно написать:

Уравнение для функции  приобретает вид:
приобретает вид:

где

Функцию  можно представить в виде:
можно представить в виде:


Поскольку полная система собственных значений и собственных функций для уравнения

была уже найдена ранее, то, пользуясь стандартными методами (см., например [20]), можно найти решение написанного выше неоднородного уравнения для  . После этого отыскание функции
. После этого отыскание функции  с помощью третьего уравнения системы (3.32) не составит труда.
с помощью третьего уравнения системы (3.32) не составит труда.
Проведенное в данной главе изучение пространственного обтекания тел указывает на то, что при обтекании препятствий потоком несжимаемой жидкости возникают вихревые образования с частотами, спектр которых дискретен. В дальнейшем структура потока определяется законами поведения вихрей. Вихревые нити представляют собой неустойчивые образования [4], распадаясь, они образуют петли, которые преобразуются в вихревые кольца, а последние, в случае значительного превышения радиуса кольца над радиусом его тела, тоже неустойчивы относительно формы. Деление колец продолжается до тех пор, пока радиус кольца не станет одного порядка с диаметром его тела. Эти новые вихревые образования за счет диффузии постепенно распространяются от места своего зарождения в соседние с поверхностью обтекаемого препятствия слои жидкости и сносятся за счет конвекции вниз по потоку.
Таким образом, вблизи обтекаемого препятствия формируется, увеличиваясь в размерах, область стохастического движения вихревых образований. При числах Рейнольдса больше 103, размеры этой области становятся сравнимыми с характерным масштабом задачи, область стохастического движения вихрей перекрывает всю область течения, которое в этом случае называют турбулентным. Если эту точку зрения принять в качестве исходной, то турбулентное движение следует считать стохастической совокупностью периодических движений, а следовательно скорость любой частицы жидкости, участвующей в таком движении может быть представлена в виде ряда Фурье. Введение средних по времени скоростей частиц жидкости или молей по терминологии Рейнольдса [21] в такой ситуации теряет смысл, т. к. средняя по времени величина периодической функции зависит от интервала осреднения. Это обстоятельство делает спорным подход Рейнольдса [21] к решению задач, связанных с турбулентными течениями, при котором скорость жидкой частицы представляют как некоторую среднюю скорость плюс скорость пульсаций.







![]() ,
,  - тензорная единица, а
- тензорная единица, а 
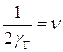 , где
, где 
 (3 1)
(3 1)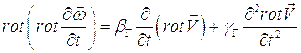
 (3.2)
(3.2)![]()

 (3.3)
(3.3) ; (3.4)
; (3.4)



![]()
 (3.5)
(3.5) ,
,  , позволяет вычислить характеристики гидромеханического поля -
, позволяет вычислить характеристики гидромеханического поля -  (3.6)
(3.6)
 для всех
для всех 


 , где
, где 

 (3.7)
(3.7)
 (3.8)
(3.8)
 (3.9)
(3.9)

![]()



 ,
, 

 (3.10)
(3.10)

![]() (3.11)
(3.11)






![]()
![]()






 выполняется, если положить
выполняется, если положить  и
и 

 (3.12)
(3.12) (3.13)
(3.13)
![]()

![]()

 ,
,
 (3.14)
(3.14)







![]()
![]()





 следует:
следует:

![]()
![]()

 (3.15)
(3.15)




 , тогда:
, тогда:


![]() ,
, ![]() ,
, ![]() ,
,  ;
;
![]()
![]()
![]() (3.16)
(3.16)

 ,
, ![]() ,
,![]()



 - безразмерное время,
- безразмерное время, 
 (3.18)
(3.18) (3.19)
(3.19) (3.20)
(3.20)




 ,
,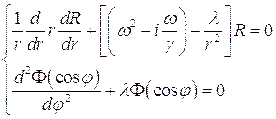 (3.21)
(3.21)

 ,
,
 и
и 
 (3.22)
(3.22)

 здесь
здесь 

 неограниченно возрастает при
неограниченно возрастает при  , где
, где  , что эквивалентно:
, что эквивалентно:
 (3.23)
(3.23)
 (3.24)
(3.24)
 (3.25)
(3.25)




![]()
 (3.28)
(3.28) 
![]() , то есть
, то есть (3.29)
(3.29)


 (3.30)
(3.30) (3.31)
(3.31)





![]() , можно воспользоваться уравнением (3.31). Таким образом, исходная система уравнений (3.28) эквивалентна следующей системе:
, можно воспользоваться уравнением (3.31). Таким образом, исходная система уравнений (3.28) эквивалентна следующей системе:  (3.32)
(3.32)![]() ;
; ![]()
![]() ,
, ![]() ; на
; на ![]() - ограничения не накладываются
- ограничения не накладываются![]() , то, при
, то, при ![]()
![]() ,
, ![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()

 (3.33)
(3.33)![]() - положительное число.
- положительное число.![]() должна удовлетворять уравнению
должна удовлетворять уравнению
![]()
![]() ,
,![]()
![]() можно представить в виде:
можно представить в виде: ![]()

![]() - положительное число.
- положительное число.![]() должна удовлетворять уравнению:
должна удовлетворять уравнению:![]()
![]()
![]() и линейно независимыми решениями этого уравнения являются:
и линейно независимыми решениями этого уравнения являются: ![]() и
и ![]() , причем
, причем ![]() - целое число.
- целое число.![]() должна удовлетворять уравнению:
должна удовлетворять уравнению:
![]() , преобразуется к уравнению присоединенных функций
, преобразуется к уравнению присоединенных функций
![]() ,
, ![]()
![]() , то решением этого уравнения будут присоединенные функции:
, то решением этого уравнения будут присоединенные функции:
![]() - полином Лежандра степени
- полином Лежандра степени ![]() ,
, ![]() .
.![]() на основании соотношения (3.33) получим:
на основании соотношения (3.33) получим:
 , преобразуем это уравнение к виду:
, преобразуем это уравнение к виду:
![]()
![]()
![]()
![]()
![]()
![]() , то для выполнения первого из этих условий необходимо:
, то для выполнения первого из этих условий необходимо: ![]()
![]() , либо
, либо ![]() .
. ![]() , а последнее из этих уравнений дает рекуррентную формулу для определения
, а последнее из этих уравнений дает рекуррентную формулу для определения ![]() по известному
по известному ![]()

![]()
![]() эта формула приобретает вид:
эта формула приобретает вид: 
![]() , где
, где ![]()

![]() будем иметь:
будем иметь: 
![]()

![]()

![]()

![]()
![]() и
и ![]() произвольные константы, могут быть выбраны в соответствие с условиями задачи
произвольные константы, могут быть выбраны в соответствие с условиями задачи

![]() и
и ![]() очевидна. Оставляя за рамками этой книги доказательства ортогональности, полноты и замкнутости функций
очевидна. Оставляя за рамками этой книги доказательства ортогональности, полноты и замкнутости функций ![]() и
и ![]() , отметим, что их построение, а следовательно и поведение при
, отметим, что их построение, а следовательно и поведение при ![]() , аналогично функциям Ханкеля первого и второго рода. Если из двух значений
, аналогично функциям Ханкеля первого и второго рода. Если из двух значений 
![]() со знаком "+", то условию ограниченности будет отвечать случай
со знаком "+", то условию ограниченности будет отвечать случай ![]() , если взять
, если взять ![]() со знаком "-", то
со знаком "-", то ![]() . Для определенности выберем знак "-", тогда для функции
. Для определенности выберем знак "-", тогда для функции ![]() справедливо:
справедливо:
![]() ;
; ![]() будут выполняться, а условие
будут выполняться, а условие ![]() выполняется, если
выполняется, если![]() , т.е.
, т.е. ![]() , где
, где ![]() - к-ый корень уравнения
- к-ый корень уравнения ![]() , отсюда
, отсюда
![]() отвечающие этому условию. Отметим, что из этого условия следует соотношение аналогичные (3.23).
отвечающие этому условию. Отметим, что из этого условия следует соотношение аналогичные (3.23). 
![]() приобретает вид:
приобретает вид: 

![]() можно представить в виде:
можно представить в виде:![]()


![]() . После этого отыскание функции
. После этого отыскание функции ![]() с помощью третьего уравнения системы (3.32) не составит труда.
с помощью третьего уравнения системы (3.32) не составит труда.
