ЧАСТЬ I.
Вихревая механика.
ГЛАВА I.
Изотермические движения несжимаемой жидкости.
Вихревые движения вязкой жидкости представляют собой объект, вызывающий наибольшие трудности при описании произвольных движений жидкости. Поэтому целесообразно дать анализ уравнений движения жидкости в общем случае, исходя из законов сохранения массы, количества движения, момента количества движения и энергии и, прежде чем переходить к рассмотрению пространственных течений вязкой жидкости, проанализировать эффективность гипотез, к которым прибегают при написании уравнений движения в частных случаях.
§1. Уравнения движения сплошной среды в интегральной и
дифференциальной формах.
В качестве исходного пункта для описания движения сплошных сред целесообразно использовать общие теоремы динамики в интегральной форме, поскольку при произвольном движении среды могут иметь место разрывы скорости, плотности и других ее параметров.
На основании закона сохранения массы в нерелятивистском случае для произвольной сплошной среды, занимающей объем  , ограниченный поверхностью
, ограниченный поверхностью  , можно записать:
, можно записать:
 (1.1)
(1.1)
где  – плотность среды,
– плотность среды,  – изменение плотности за единицу времени в данной точке за счет внутренних источников (стоков) вещества.
– изменение плотности за единицу времени в данной точке за счет внутренних источников (стоков) вещества.
Изменение количества движения среды можно вычислить согласно:
 (1.2)
(1.2)
где  - скорость среды,
- скорость среды,  - главный вектор внешних массовых сил,
- главный вектор внешних массовых сил,  – тензор напряжений, приложенных к поверхности
– тензор напряжений, приложенных к поверхности  объема
объема  ,
,  - единичный вектор, направленный по нормали к элементарной площадке
- единичный вектор, направленный по нормали к элементарной площадке  .
.
Изменение момента количества движения можно вычислить, пользуясь равенством:
 (1.3)
(1.3)
где  - радиус-вектор, характеризующий положение материальной точки среды, квадратными скобками обозначены векторные произведения.
- радиус-вектор, характеризующий положение материальной точки среды, квадратными скобками обозначены векторные произведения.
Изменение полной энергии среды можно вычислить, пользуясь общим термодинамическим законом сохранения полной энергии системы:
 (1.4)
(1.4)
здесь:  – удельная внутренняя энергия среды,
– удельная внутренняя энергия среды,
 – удельное количество энергии, подведенное в единицу времени к данной точке среды извне.
– удельное количество энергии, подведенное в единицу времени к данной точке среды извне.
В том случае, когда входящие в уравнения (1.1 – 1.4) функции непрерывны и дифференцируемы, эти уравнения можно преобразовать в систему уравнений движения среды в дифференциальной форме. Это условие означает, что уравнения движения в дифференциальной форме можно использовать для описания движения только таких сред, параметры которых терпят разрывы лишь на границе  , рассматриваемой области
, рассматриваемой области  , или за ее пределами. Дальнейшее изложение в данной главе исходит из этого предположения.
, или за ее пределами. Дальнейшее изложение в данной главе исходит из этого предположения.
Поскольку

то уравнение (1.1) примет вид:

или
 (1.5)
(1.5)
В уравнении (1.2) преобразуем поверхностный интеграл в объемный, воспользовавшись формулами векторного анализа

Кроме того, примем во внимание, что

следовательно

отсюда

или
 (1.6)
(1.6)
В уравнении (1.3) преобразуем левую часть:

а затем второе слагаемое в правой части уравнения (1.3):

с учетом полученных соотношений уравнение (1.3) можно преобразовать к виду:

Воспользовавшись (1.6) найдем, что первое слагаемое в этом уравнении равно нулю. Если учесть, что объем  может быть выбран произвольно и, кроме того,
может быть выбран произвольно и, кроме того,

получим, что

или, спроектировав это уравнение на оси координат:

Это означает, что тензор напряжений  симметричен
симметричен  . Отметим, что полученный вывод есть следствие уравнения (1.3) , в основу которого положено предположение об отсутствии в среде непрерывно распределенных объемных или поверхностных пар сил, то есть имеет место так называемая симметричная механика сплошных сред. Дальнейшее изложение исходит из этого предположения.
. Отметим, что полученный вывод есть следствие уравнения (1.3) , в основу которого положено предположение об отсутствии в среде непрерывно распределенных объемных или поверхностных пар сил, то есть имеет место так называемая симметричная механика сплошных сред. Дальнейшее изложение исходит из этого предположения.
Выполним аналогичные преобразования в уравнении (1.4):

и соответственно уравнение (1.4) примет вид:
 (1.7)
(1.7)
Таким образом, если внутри изучаемого объема сплошной среды отсутствуют разрывы непрерывности характеризующих состояние среды функций и их производных, то для описания движения такой среды можно использовать систему дифференциальных уравнений, состоящую из уравнений (1.5, 1.6, 1.7), в которой  есть симметричный тензор напряжений.
есть симметричный тензор напряжений.
§2. Дифференциальные уравнения движения несжимаемой среды.
Преобразуем уравнение (1.7) воспользовавшись тем, что

где дифференциальный тензор

В результате получим:

или, с учетом (1.6):
 (1.8)
(1.8)
Отметим, что дифференциальный тензор  можно разложить на симметричную часть
можно разложить на симметричную часть  (тензор скоростей деформаций) и антисимметричную
(тензор скоростей деформаций) и антисимметричную  .
.
Поскольку тензор  - антисимметричен, то
- антисимметричен, то  ,
,
то есть

где  - тензор скоростей деформаций, компоненты которого
- тензор скоростей деформаций, компоненты которого

Аналогично тому, как в механике дискретных материальных точек мощность есть скалярное произведение вектора силы на вектор скорости, в механике сплошных сред скалярное произведение тензора напряжений на тензор скоростей деформаций есть плотность распределения мощности внутренних сил, следовательно, последнее слагаемое в полученном уравнении следует рассматривать как плотность распределения мощности внутренних сил.
Обратимся теперь к описанию движения сплошной среды, в которой отсутствуют источники (стоки) массы  и тепла
и тепла  , а внутренняя энергия ее не зависит от времени
, а внутренняя энергия ее не зависит от времени  . Уравнения (1.6) и (1.7) в этом случае принимают идентичный вид:
. Уравнения (1.6) и (1.7) в этом случае принимают идентичный вид:

Если и плотность не зависит от времени, то из (1.5) следует:

Таким образом, движение сплошной среды, не содержащей разрывов параметров и источников (стоков) массы и тепла, плотность и внутренняя энергия которой не изменяются во времени, должно описываться системой уравнений:
 (1.9)
(1.9)
где  – симметричный тензор.
– симметричный тензор.
Вместе с тем необходимо указать, что эта система уравнений в общем случае не является замкнутой, поскольку содержит шесть неизвестных скалярных величин (три компоненты вектора скорости и три компоненты вектора  ) и только четыре скалярных уравнения, то есть для описания движения среды в этом случае недостаточно только уравнений, вытекающих из общих законов сохранения массы, количества движения, момента количества движения и энергии. Это обстоятельство указывает на то, что уравнения (1.9) должны быть дополнены соотношениями, отражающими взаимодействие между элементами сплошной среды, в частности, отражающими распространение возмущений, порождаемых движущимися элементами среды.
) и только четыре скалярных уравнения, то есть для описания движения среды в этом случае недостаточно только уравнений, вытекающих из общих законов сохранения массы, количества движения, момента количества движения и энергии. Это обстоятельство указывает на то, что уравнения (1.9) должны быть дополнены соотношениями, отражающими взаимодействие между элементами сплошной среды, в частности, отражающими распространение возмущений, порождаемых движущимися элементами среды.
§3. Потенциальные течения жидкости.
Наиболее простым приемом, позволяющим превратить систему уравнений (1.9) в замкнутую, является предположение о том, что движение среды не сопровождается возникновением вихрей. В этом случае для любой точки среды справедливо:

этому условию эквивалентно:

где  - скалярная функция, которую называют потенциалом скоростей, а течение - потенциальным.
- скалярная функция, которую называют потенциалом скоростей, а течение - потенциальным.
Поскольку, согласно правилам векторного анализа:  , то нетрудно видеть, что для потенциальных течений несжимаемой жидкости с учетом уравнения неразрывности справедливо:
, то нетрудно видеть, что для потенциальных течений несжимаемой жидкости с учетом уравнения неразрывности справедливо:

отсюда следует, что вместо системы уравнений (1.9) в случае потенциальных течений целесообразно использовать:
 (1.10)
(1.10)
Первому уравнению этой системы, воспользовавшись соотношением:
 , можно придать форму уравнения Громеки-Лэмба:
, можно придать форму уравнения Громеки-Лэмба:
 (1.11)
(1.11)
Если объемные силы имеют потенциал, то есть  , то оно приобретает вид:
, то оно приобретает вид:

Для безвихревых течений отсюда следует:
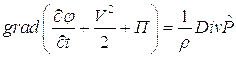
Это равенство возможно, если
 или
или 
где  - тензорная единица,
- тензорная единица,  – скалярная величина.
– скалярная величина.
Отсюда следует, что нормальное напряжение, приложенное к элементарной площадке в данной точке, не зависит от направления площадки. Если эту величину положить равной давлению, определенному также, как в гидростатике и термодинамике, то первое из уравнений системы (1.10) принимает вид:
 (1.12)
(1.12)
Это уравнение называют уравнением Эйлера, а жидкость, движение которой можно описать с помощью этого уравнения – идеальной. В этом случае после интегрирования предыдущего уравнения получим интеграл Лагранжа-Коши:

здесь  – функция времени, определяемая с помощью граничных условий, одинаковая для всей области течения.
– функция времени, определяемая с помощью граничных условий, одинаковая для всей области течения.
В стационарном случае:  , этот интеграл превращается в уравнение Бернулли:
, этот интеграл превращается в уравнение Бернулли:
 (1.13)
(1.13)
Назовем линией тока линию, касательная к которой в каждой точке совпадает с линией действия вектора скорости. В стационарном случае линии тока совпадают с траекториями частиц жидкости. Рассмотрим произвольный не пересекающий себя и не имеющий особых точек замкнутый контур, проходящий в данный момент времени через точки жидкости. Проведем через каждую его точку линию тока. Совокупность всех линий тока, проходящих через данный контур будем называть поверхностью тока, часть жидкости, заключенную внутри такой поверхности – трубкой тока, а поверхность, расположенную внутри трубки тока и опирающуюся на заданный контур – сечением трубки. Если сечение трубки настолько мало, что изменением скорости в его пределах можно пренебречь, то будем называть такую трубку элементарной.
Рассмотрим одномерное течение, такое, в котором линии тока заданы, а следовательно скорость, как и сечение трубки тока -  , зависят только от одной, в общем случае криволинейной координаты –
, зависят только от одной, в общем случае криволинейной координаты –  . Система уравнений (1.10), с учетом изложенного, преобразуется к виду:
. Система уравнений (1.10), с учетом изложенного, преобразуется к виду:

здесь индекс 0 означает, что значение величины следует взять в сечении, принятом за начальное. Из этих уравнений следует:

Таким образом, параметры одномерного потока могут быть однозначно определены, если известны значения скорости и давления в некотором сечении, принятом за начальное, а также зависимость площади сечения от координаты -  . Полученные соотношения указывают на то, что границы, влияя на величину сечения трубки, тем самым влияют на величину скорости, а значит непосредственно влияют на величину давления даже в случае безвихревых течений несжимаемой жидкости.
. Полученные соотношения указывают на то, что границы, влияя на величину сечения трубки, тем самым влияют на величину скорости, а значит непосредственно влияют на величину давления даже в случае безвихревых течений несжимаемой жидкости.
В случае плоских течений условие  сводится к уравнению:
сводится к уравнению:

Используя это соотношение, из второго уравнения системы (1.10) нетрудно получить:

откуда следует:

Поскольку источники (стоки) массы отсутствуют, то  , следовательно в случае плоских безвихревых течений вместо второго уравнения системы (1.10) можно пользоваться системой уравнений:
, следовательно в случае плоских безвихревых течений вместо второго уравнения системы (1.10) можно пользоваться системой уравнений:

Эти уравнения позволяют ввести функции:  – потенциал скоростей,
– потенциал скоростей,  – функцию тока, такие, что
– функцию тока, такие, что

отсюда следует, что потенциал скоростей и функция тока удовлетворяют условиям Коши-Римана:

которые означают, что величина

является функцией одной комплексной переменной  , а это позволяет утверждать, что
, а это позволяет утверждать, что

Функцию  называют комплексным потенциалом или характеристической функцией течения, а проекции скорости на оси абсцисс и ординат определяются как, соответственно, действительная и умноженная на минус единицу мнимая части производной, взятой от характеристической функции по комплексной переменной.
называют комплексным потенциалом или характеристической функцией течения, а проекции скорости на оси абсцисс и ординат определяются как, соответственно, действительная и умноженная на минус единицу мнимая части производной, взятой от характеристической функции по комплексной переменной.
Таким образом, задача о плоских безвихревых течениях сводится к решению системы уравнений:
 (1.14)
(1.14)
Решение этой системы уравнений не представляет труда, если известны функции  . В частности для однородного потока, вектор скорости которого
. В частности для однородного потока, вектор скорости которого  направлен под углом
направлен под углом  к оси Ох, комплексный потенциал имеет вид:
к оси Ох, комплексный потенциал имеет вид:

Однако следует указать, что отыскание упомянутых функций не встречает трудностей в том случае, если область течения является односвязной, т.е. такой, что все взятые в ней замкнутые кривые приводимы, то есть могут быть стянуты в точку, оставаясь внутри области. Вычислим в этом случае криволинейный интеграл вдоль произвольной кривой  :
:

Замкнем кривую  кривой
кривой  , не совпадающей с первой. Если рассматриваемая область односвязна, то замкнутый контур
, не совпадающей с первой. Если рассматриваемая область односвязна, то замкнутый контур  , образованный кривыми
, образованный кривыми  и
и  может быть стянут в точку и циркуляция скорости по этому контуру:
может быть стянут в точку и циркуляция скорости по этому контуру:

Следовательно, в этом случае функция потенциала скоростей есть однозначная функция координат и можно использовать для отыскания поля скоростей изложенную выше методику. Вместе с тем можно показать [13], что если на границе односвязной области скорость жидкости равна нулю, то жидкость в такой области покоится. Это обстоятельство делает проблематичным адекватное описание движения реальных жидкостей, поскольку опытные данные свидетельствуют о "прилипании" жидкостей к твердым поверхностям, ограничивающим ее движение. Для описания течения жидкости в этом случае можно использовать введение в рассматриваемую область источников (стоков) массы или вихрей, занимающих пренебрежимо малую часть этой области, однако это нарушает потенциальность течения жидкости. Во избежание этого такие источники можно ограничить поверхностями, а образовавшиеся внутри них области исключить из рассмотрения. Однако получившаяся после такой операции область движения жидкости перестает быть односвязной, а, следовательно, циркуляция жидкости по контуру, охватывающему источники, отлична от нуля, а это означает, что ее значение зависит от формы контура, то есть циркуляция скорости станет неоднозначной функцией. Область течения жидкости можно сделать односвязной с помощью введения  перегородок, где
перегородок, где  – порядок связности области, значения циркуляции скорости по обе стороны перегородки будут отличаться на постоянную величину, которая называется циклической постоянной [4]. Аналогичное замечание следует сделать и относительно функции тока.
– порядок связности области, значения циркуляции скорости по обе стороны перегородки будут отличаться на постоянную величину, которая называется циклической постоянной [4]. Аналогичное замечание следует сделать и относительно функции тока.
Обозначим:
 - циклическая постоянная циркуляции скорости,
- циклическая постоянная циркуляции скорости,
 - секундный объемный расход жидкости через контур.
- секундный объемный расход жидкости через контур.
Комплексные потенциалы для простейших течений можно представить в виде:
- Источник (сток) в начале координат, секундный расход которого
 – действительная величина, положительная в случае источника и отрицательная в случае стока
– действительная величина, положительная в случае источника и отрицательная в случае стока

- Изолированный вихрь, расположенный в начале координат с циркуляцией


- Диполь с моментом
 , расположенный в начале координат с осью, направленной вдоль оси Ох
, расположенный в начале координат с осью, направленной вдоль оси Ох

Поскольку второе уравнение системы (1.14) является линейным, то можно воспользоваться приемом наложения потоков и получить комплексные потенциалы для вихреисточника, бесциркулярного и циркулярного обтекания круглого цилиндра. Например, потенциал обтекания круглого цилиндра, можно записать в виде суммы потенциалов вихря с циркуляцией  и бесциркулярного обтекания цилиндра:
и бесциркулярного обтекания цилиндра:

Изложенный подход можно использовать и для описания пространственных безвихревых течений. Для простых движений жидкости удается найти вид потенциала скоростей, в частности:
- прямолинейное однородное течение безграничной жидкости, скорость которого
 составляет углы
составляет углы  с декартовыми осями
с декартовыми осями
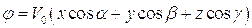
- источник (сток) жидкости в начале отсчета, находящийся в неограниченной жидкости

здесь  – мощность потока,
– мощность потока,  – расстояние от источника до заданной точки.
– расстояние от источника до заданной точки.
- диполь с моментом
 в неограниченной жидкости, помещенной в начало отсчета
в неограниченной жидкости, помещенной в начало отсчета

здесь  – угол между линиями, соединяющими данную точку с полюсами диполя.
– угол между линиями, соединяющими данную точку с полюсами диполя.
Функцию тока для пространственных движений жидкости в общем случае ввести невозможно. Она может быть определена в отдельных случаях, в частности, ее можно ввести, если имеет место симметрия относительно одной из осей координат, и одна из компонент скорости жидкости либо равна нулю, либо не зависит от одной из координат, а, следовательно, введение функции тока зависит не только от вида течения, но и от типа системы координат, в которой рассматривается течение. Приведенные выше примеры отвечают этим условиям; в сферической системе координат функции тока имеют вид:
- для однородного прямолинейного потока –

- для источника (стока) мощностью
 –
–

- для диполя с моментом
 –
–

Изложенная выше методика позволяет с помощью построения потенциала скоростей и функции тока решать задачи о безвихревом течении жидкости в каналах осесимметричной формы, а также о продольном осесимметиричном и поперечном перпендикулярном к оси симметрии обтекании жидкостью тел вращения. Комбинация последних двух позволяет построить решение задачи о поперечном обтекании тел вращения под любым углом атаки. Вместе с тем, оказывается, что при обтекании тела конечного размера безвихревым потоком идеальной несжимаемой жидкости в отсутствии источников (стоков) массы главный вектор сил давления со стороны потока на тело равен нулю.
Этот эффект, который обычно называют парадоксом Даламбера, обусловлен тем, что теоретическое рассмотрение безвихревого течения тела (для определенности, например, сферы) предполагает, что потоки жидкости, встречающиеся за телом, имеют равные нулю вдоль линии, проходящей через центр тела и параллельной скорости набегающего потока, составляющие скорости перпендикулярные этой линии. Однако достаточно небольших флуктуаций скорости, чтобы это условие перестало выполняться, и возник вихрь. Парадокс Даламбера свидетельствует о том, что реально обтекание тела конечного размера не может быть потенциальным, непосредственно за телом возникает вихревое движение жидкости.
Необходимо иметь в виду еще одно обстоятельство, которое затрудняет использование модели потенциального течения для описания реальных движений жидкости. При обтекании непроницаемой стенки должна быть положена равной нулю нормальная к стенке составляющая скорости, а для потенциального течения это означает, что устанавливается и касательная к стенке составляющая скорости. Следовательно, отражающее течение реальной жидкости условие прилипания жидкости к стенке, то есть условие равенства нулю касательной составляющей, в общем случае не может быть выполнено, а это делает проблематичным использование потенциальных течений для описания всего многообразия движений реальных жидкостей.
§4. Вязкое течение жидкости.
Практика и экспериментальные исследования свидетельствуют, что жидкость прилипает к поверхностям, ограничивающим ее движение. В потоке жидкости возникает перепад скоростей: от скорости, равной скорости поверхности, до скорости на большом удалении от нее, обусловленный взаимодействием слоев жидкости, которое принято называть внутренним трением или вязкостью жидкости. Совокупность представлений о безвихревых движениях жидкости не позволяет адекватно описать течение взаимодействующих слоев жидкости.
Наиболее простым способом, позволяющим учесть влияние вязкости жидкости, является полуэмпирический подход. Уравнение Бернулли остается справедливым вдоль линии тока и для вязкой жидкости [14]. В реальном потоке скорость жидкости меняется от струйки к струйке. В результате их взаимодействия часть механической энергии расходуется на преодоление внутреннего трения. Эту часть энергии учитывают, вводя потерю напора на трение  .
.
Интегрируя в двух сечениях уравнение (1.13) по живому сечению потока, можно получить:

здесь:
 -скоростной напор или удельная кинетическая энергия,
-скоростной напор или удельная кинетическая энергия,
 - высота давления или пьезометрическая высота,
- высота давления или пьезометрическая высота,
 – высота положения или геометрическая высота,
– высота положения или геометрическая высота,
 – корректив скорости, показывающий насколько средняя скорость, вычисленная по расходу, отличается от скорости, осредненной по сечению,
– корректив скорости, показывающий насколько средняя скорость, вычисленная по расходу, отличается от скорости, осредненной по сечению,
 – расходная скорость.
– расходная скорость.
Различают потери напора двух типов: потери на трение вдоль потока и потери, локализованные на участках изменения сечения потока или его разделения (слияния), так называемые внешние потери. Для расчета потерь напора вдоль трубопровода применяют формулу Дарси:

где  – коэффициент сопротивления,
– коэффициент сопротивления,
 – диаметр трубопровода,
– диаметр трубопровода,
 – длина трубопровода.
– длина трубопровода.
Для расчета местных потерь используют эмпирическую формулу Вейсбаха:

где  – коэффициент местных потерь.
– коэффициент местных потерь.
Коэффициент местных потерь определяется видом элемента трубопровода, его значения лежат в пределах 0,1 7. Коэффициент сопротивления зависит от вязкости жидкости, ее скорости и шероховатости стенок трубопровода и может быть определен с помощью эмпирических зависимостей. Изложенный подход позволяет учесть потери на внутреннее трение, однако не вскрывает механизма влияния вязкости на картину течения.
7. Коэффициент сопротивления зависит от вязкости жидкости, ее скорости и шероховатости стенок трубопровода и может быть определен с помощью эмпирических зависимостей. Изложенный подход позволяет учесть потери на внутреннее трение, однако не вскрывает механизма влияния вязкости на картину течения.
Рассмотрение системы уравнений (1.9) показывает, что она становится замкнутой, если, сохранив предположение о потенциальном характере объемных сил, принять гипотезу, восходящую к Ньютону и состоящую в том, что сила трения между струйками жидкости пропорциональна градиенту скорости в направлении, перпендикулярном линии тока. В обобщенной форме эту зависимость можно представить в виде линейной связи между тензором напряжений и тензором скоростей деформаций:
 (1.15)
(1.15)
где  - тензор скоростей деформаций,
- тензор скоростей деформаций,
 - единичный тензор,
- единичный тензор,
 – скалярная величина, равная давлению, понимаемому также, как в гидростатике и термодинамике,
– скалярная величина, равная давлению, понимаемому также, как в гидростатике и термодинамике,
 – коэффициент пропорциональности, который называют динамическим коэффициентом вязкости.
– коэффициент пропорциональности, который называют динамическим коэффициентом вязкости.
Это соотношение можно представить в развернутом виде:

В прямоугольной декартовой системе координат соотношение (1.15) эквивалентно системе скалярных уравнений:

Система уравнений (1.8) может быть записана в виде:

Используя выражения для компонент тензора давления, записанные выше, преобразуем правые части этих уравнений. В частности, в правой части первого уравнения:

Аналогично для второго и третьего уравнений:

Следовательно, система уравнений (1.8) принимает вид:

или, поделив обе части первого уравнения на  :
:
 (1.16)
(1.16)
где  - коэффициент кинематической вязкости.
- коэффициент кинематической вязкости.
Эти уравнения называют уравнениями Навье-Стокса. Они представляют собой замкнутую систему уравнений в частных производных второго порядка, поскольку массовые силы  обычно считают известными потенциальными силами, а
обычно считают известными потенциальными силами, а  является скалярной величиной.
является скалярной величиной.
Стационарные уравнения Навье-Стокса, то есть записанные для случая  , успешно используется для описания медленных течений жидкости в трубах, при обтекании шара, течения между коаксиальными цилиндрами. В результате решений этих уравнений можно получить закон Пуазейля для определения расхода жидкости через трубу и формулу Стокса для определения сопротивления шара.
, успешно используется для описания медленных течений жидкости в трубах, при обтекании шара, течения между коаксиальными цилиндрами. В результате решений этих уравнений можно получить закон Пуазейля для определения расхода жидкости через трубу и формулу Стокса для определения сопротивления шара.
Прандтль использовал уравнения Навье-Стокса для описания движения жидкостей, обладающих малой вязкостью, в непосредственной близости от плоских твердых поверхностей. Полагая, что в этом случае скорость жидкости быстро уменьшается от скорости основного потока до нуля на поверхности в весьма тонком пограничном слое, а потому давление поперек пограничного слоя меняется несущественно, и производная по координате от компонента скорости вдоль по потоку изменяется мало по сравнению с ее производной по координате поперек потока, Прандтль положил

и преобразовал стационарные уравнения Навье-Стокса к уравнениям:

с граничными условиями:

где  – скорость во внешнем потоке,
– скорость во внешнем потоке,
Обычно считают, что роль вязкости во внешнем потоке, прилегающем к пограничному слою, мала, поэтому здесь справедлив закон Бернулли, а, следовательно, можно положить:

Система уравнений пограничного слоя Прандтля принимает вид:

Отметим, что если придать форму Громеки-Лэмба уравнению Навье-Стокса, то оно примет вид:

В то время как уравнение Эйлера в этом случае имеет вид:

При переходе к невязким течениям следует в стационарном уравнении Навье-Стокса положить  , и оно приобретает вид:
, и оно приобретает вид:


тогда как при переходе к потенциальным течениям в уравнении Эйлера полагают  , поэтому оно примет вид:
, поэтому оно примет вид:

В общем случае эти два различных уравнения дают различные решения, поэтому нет строгих оснований для совместного решения уравнений, входящих в систему уравнений пограничного слоя, что делает сомнительным их использование при описании реальных течений жидкости.
Подчеркнем, что система уравнений (1.16) строго справедлива, если внутренняя энергия системы не изменяется. При отсутствии источников (стоков) массы и подведения извне энергии к среде для изменения внутренней энергии на основании (1.8) можно записать:

В данном случае:

Полагая  этому выражению можно придать вид:
этому выражению можно придать вид:

где  - тензор скоростей деформаций.
- тензор скоростей деформаций.
Таким образом:

Следовательно, уравнения (1.16) можно использовать только для описания течений с достаточно малыми скоростями, когда можно считать, что  .
.
Принято считать, что обтекание тел вязкой жидкостью может быть адекватно описано с помощью уравнений Навье-Стокса, и только математические трудности препятствуют решению таких задач. Однако в этом возникают сомнения, если сопоставить нестационарные уравнения Навье-Стокса и Эйлера, записанные в форме Громеки-Лэмба:


Полагая, что объемные силы имеют потенциал  и, применив к обеим частям этих уравнений операцию
и, применив к обеим частям этих уравнений операцию  , видим, что написанные уравнения принимают аутентичный вид:
, видим, что написанные уравнения принимают аутентичный вид:

где 
Полученное уравнение не содержит коэффициента вязкости, что делает призрачными надежды на исчерпывающее описание с помощью уравнений Навье-Стокса всего комплекса движений вязкой жидкости.




![]() , ограниченный поверхностью
, ограниченный поверхностью ![]() , можно записать:
, можно записать: (1.1)
(1.1)![]() – плотность среды,
– плотность среды, ![]() – изменение плотности за единицу времени в данной точке за счет внутренних источников (стоков) вещества.
– изменение плотности за единицу времени в данной точке за счет внутренних источников (стоков) вещества. (1.2)
(1.2)![]() - скорость среды,
- скорость среды, ![]() - главный вектор внешних массовых сил,
- главный вектор внешних массовых сил, ![]() – тензор напряжений, приложенных к поверхности
– тензор напряжений, приложенных к поверхности ![]() объема
объема ![]() ,
, ![]() - единичный вектор, направленный по нормали к элементарной площадке
- единичный вектор, направленный по нормали к элементарной площадке ![]() .
. (1.3)
(1.3)![]() - радиус-вектор, характеризующий положение материальной точки среды, квадратными скобками обозначены векторные произведения.
- радиус-вектор, характеризующий положение материальной точки среды, квадратными скобками обозначены векторные произведения. (1.4)
(1.4)![]() – удельная внутренняя энергия среды,
– удельная внутренняя энергия среды, ![]() – удельное количество энергии, подведенное в единицу времени к данной точке среды извне.
– удельное количество энергии, подведенное в единицу времени к данной точке среды извне.![]() , рассматриваемой области
, рассматриваемой области ![]() , или за ее пределами. Дальнейшее изложение в данной главе исходит из этого предположения.
, или за ее пределами. Дальнейшее изложение в данной главе исходит из этого предположения.
![]()
![]() (1.5)
(1.5)



 (1.6)
(1.6)


![]() может быть выбран произвольно и, кроме того,
может быть выбран произвольно и, кроме того,
![]()
![]()
![]() симметричен
симметричен ![]() . Отметим, что полученный вывод есть следствие уравнения (1.3) , в основу которого положено предположение об отсутствии в среде непрерывно распределенных объемных или поверхностных пар сил, то есть имеет место так называемая симметричная механика сплошных сред. Дальнейшее изложение исходит из этого предположения.
. Отметим, что полученный вывод есть следствие уравнения (1.3) , в основу которого положено предположение об отсутствии в среде непрерывно распределенных объемных или поверхностных пар сил, то есть имеет место так называемая симметричная механика сплошных сред. Дальнейшее изложение исходит из этого предположения.![]()
 (1.7)
(1.7)![]() есть симметричный тензор напряжений.
есть симметричный тензор напряжений.![]()


 (1.8)
(1.8)![]() можно разложить на симметричную часть
можно разложить на симметричную часть ![]() (тензор скоростей деформаций) и антисимметричную
(тензор скоростей деформаций) и антисимметричную ![]() .
.![]() - антисимметричен, то
- антисимметричен, то ![]() ,
, ![]()
 - тензор скоростей деформаций, компоненты которого
- тензор скоростей деформаций, компоненты которого

 (1.9)
(1.9)![]()
![]()
![]() - скалярная функция, которую называют потенциалом скоростей, а течение - потенциальным.
- скалярная функция, которую называют потенциалом скоростей, а течение - потенциальным.![]() , то нетрудно видеть, что для потенциальных течений несжимаемой жидкости с учетом уравнения неразрывности справедливо:
, то нетрудно видеть, что для потенциальных течений несжимаемой жидкости с учетом уравнения неразрывности справедливо:![]()
 (1.10)
(1.10)![]() , можно придать форму уравнения Громеки-Лэмба:
, можно придать форму уравнения Громеки-Лэмба: (1.11)
(1.11)
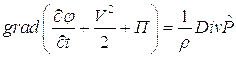
![]() или
или ![]()
 - тензорная единица,
- тензорная единица,  (1.12)
(1.12)
 (1.13)
(1.13)








 (1.14)
(1.14)
![]() - циклическая постоянная циркуляции скорости,
- циклическая постоянная циркуляции скорости,![]() - секундный объемный расход жидкости через контур.
- секундный объемный расход жидкости через контур.

![]()
![]() – мощность потока,
– мощность потока, ![]() – расстояние от источника до заданной точки.
– расстояние от источника до заданной точки.![]()
![]()
![]()
![]()
 .
.
![]() -скоростной напор или удельная кинетическая энергия,
-скоростной напор или удельная кинетическая энергия,![]() - высота давления или пьезометрическая высота,
- высота давления или пьезометрическая высота,![]() – высота положения или геометрическая высота,
– высота положения или геометрическая высота,![]() – корректив скорости, показывающий насколько средняя скорость, вычисленная по расходу, отличается от скорости, осредненной по сечению,
– корректив скорости, показывающий насколько средняя скорость, вычисленная по расходу, отличается от скорости, осредненной по сечению,![]() – расходная скорость.
– расходная скорость.







 (1.16)
(1.16) , успешно используется для описания медленных течений жидкости в трубах, при обтекании шара, течения между коаксиальными цилиндрами. В результате решений этих уравнений можно получить закон Пуазейля для определения расхода жидкости через трубу и формулу Стокса для определения сопротивления шара.
, успешно используется для описания медленных течений жидкости в трубах, при обтекании шара, течения между коаксиальными цилиндрами. В результате решений этих уравнений можно получить закон Пуазейля для определения расхода жидкости через трубу и формулу Стокса для определения сопротивления шара.












![]() и, применив к обеим частям этих уравнений операцию
и, применив к обеим частям этих уравнений операцию ![]() , видим, что написанные уравнения принимают аутентичный вид:
, видим, что написанные уравнения принимают аутентичный вид:![]()


